A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ.
The correct Answer is:R bisects the arc PQ.
Step by step video, text & image solution for A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - LONG ANSWER Type Questions13videos
CIRCLES
- BOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - SHORT ANSWER (SA-I) Type Questions28videos
CIRCLES
- BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 2EXERCISE - Section -C7videos
CBSE TERM-1 SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - LONG ANSWER Type Questions6videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−a - Question 2 - Select One
If the length of a chord of a circle , which makes a angle 45∘ with the tangent drawn at one end point of the chord , is 6 cm , then the radius of the circle is :
A6√2 cmB5 cmC3√2 cmD6 cm - Question 3 - Select One
A chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
A30∘B45∘C60∘D75∘
Prove that the length of the tangents drawn from an external point to a circle are equal.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
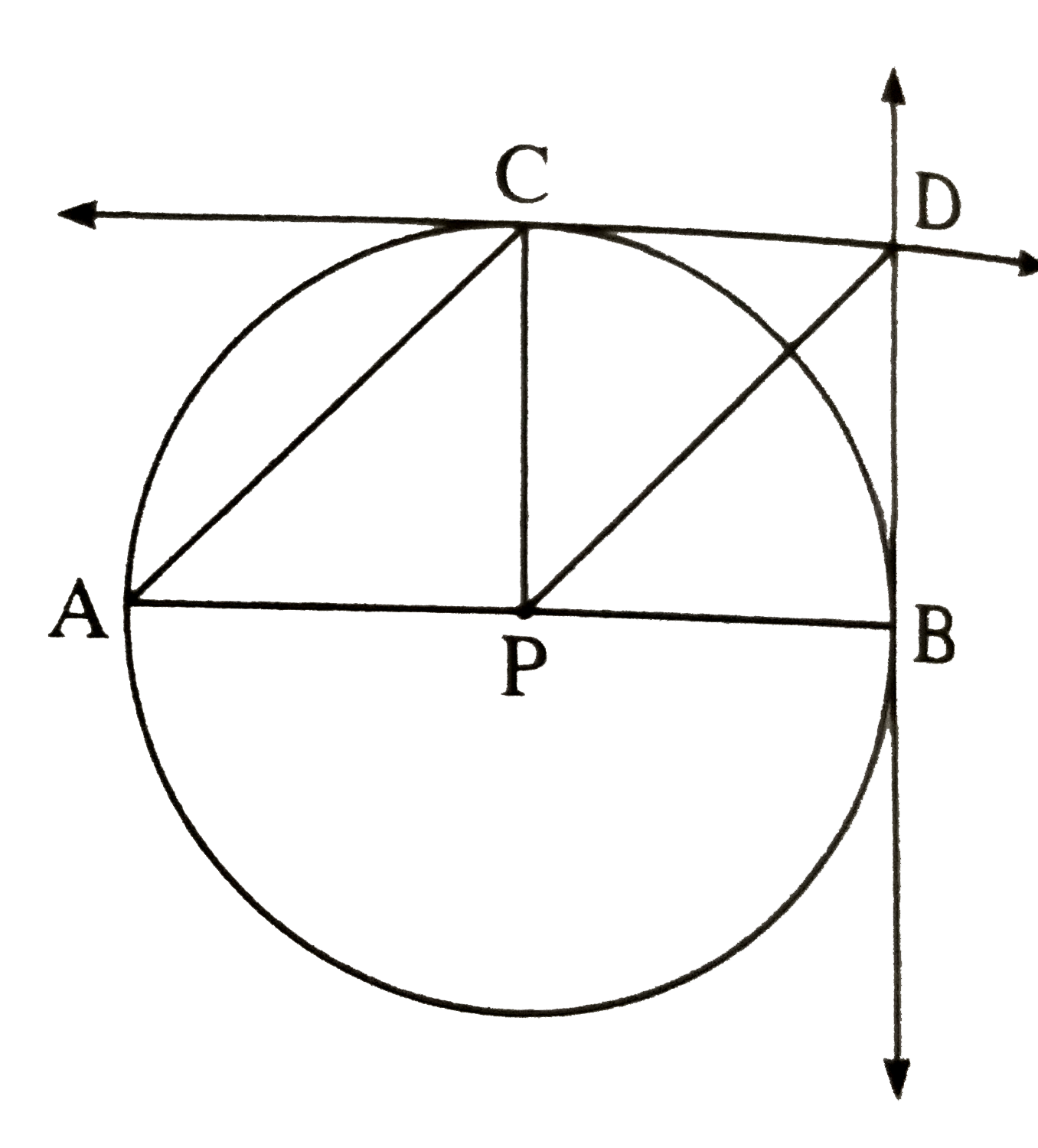 View Solution
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionTangents are drawn at extremities AB of a diameter of a circle centred at P. If tangents drawn at a point C on the circle meet the other two tangents respectively at Q and R then measure of ∠QPR is
View Solution

