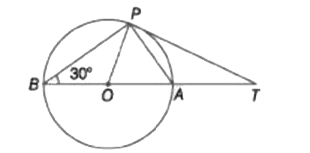
In the given figure, O is the centre of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If ∠PBO=30∘,then ∠PTA is equal to
The correct Answer is:∠TPA=30∘
Step by step video, text & image solution for In the given figure, O is the centre of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If angle PBO = 30^@,then angle PTA is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBook:EDUCART PUBLICATIONChapter:CIRCLESExercise:LONG ANSWER Type Questions
Explore 13 Videos
- CIRCLESBook:EDUCART PUBLICATIONChapter:CIRCLESExercise:SHORT ANSWER (SA-I) Type Questions
Explore 28 Videos
- CBSE TERM-1 SAMPLE PAPER 2Book:EDUCART PUBLICATIONChapter:CBSE TERM-1 SAMPLE PAPER 2Exercise:Section -C
Explore 7 Videos
- CONSTRUCTIONSBook:EDUCART PUBLICATIONChapter:CONSTRUCTIONSExercise:LONG ANSWER Type Questions
Explore 6 Videos
Similar Questions
Knowledge Check
In figure , BOA is a diameter of circle and the tangent at point P meets BA produced at. T if ∠PBO=30∘ then ∠PTA=
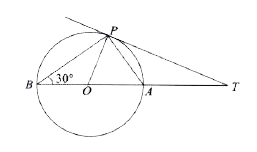 A30∘B60∘C90∘D45∘
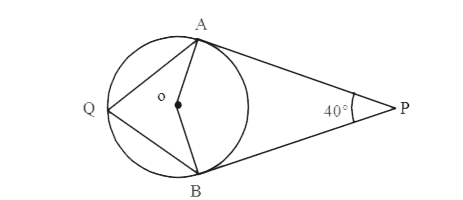
A30∘B60∘C90∘D45∘In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the figure, O is the centre of the circle . ∠PQR is equal to
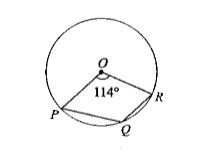 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘
In the following figure, O is the centre of the circle , AC is the diameter and if ∠APB=120∘ , then find ∠BQC .
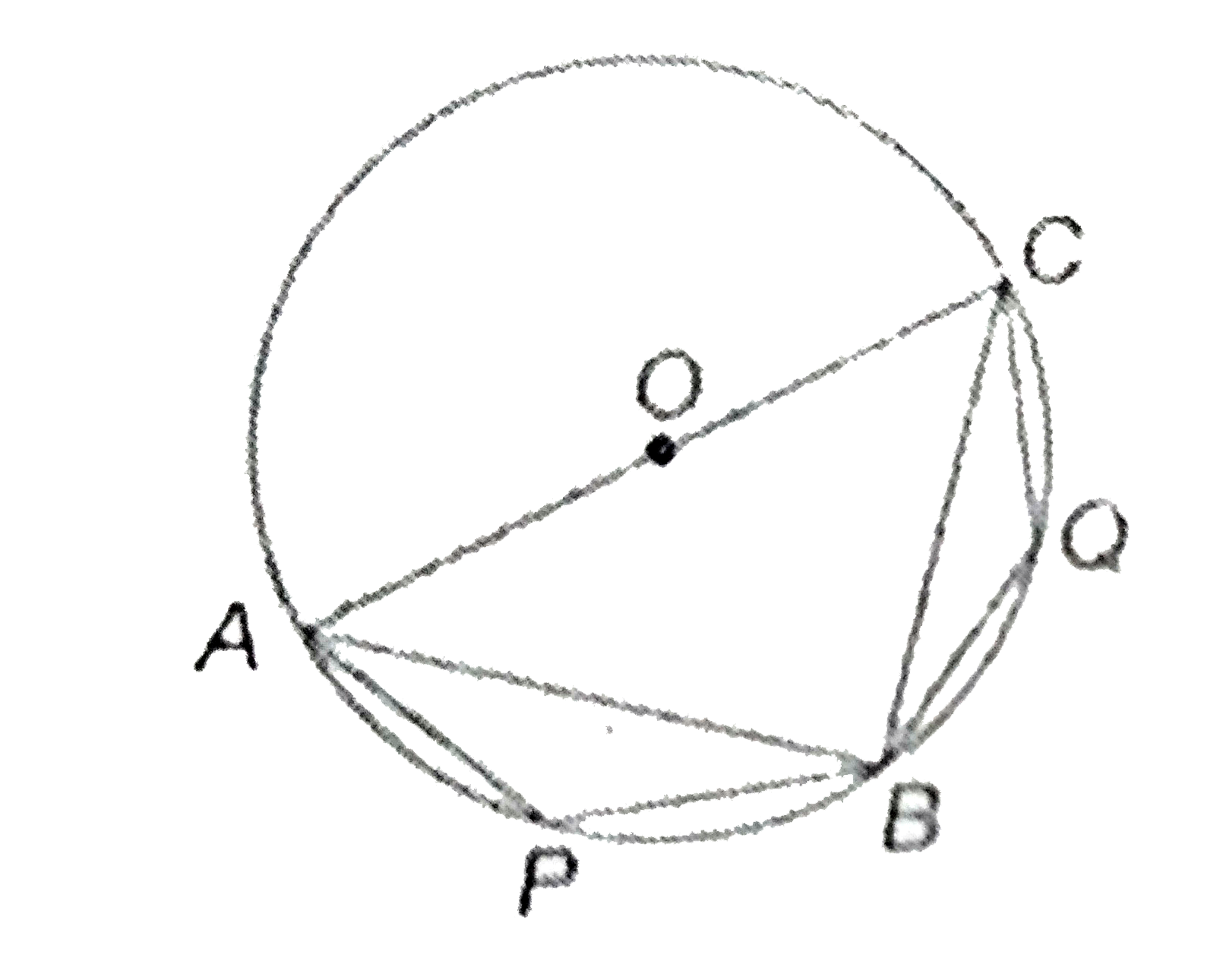
View SolutionIn the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT=30∘, prove that BA:AT =2:1
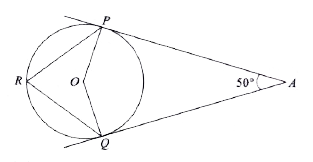
View SolutionIn the given figure ,'O is the centre of circle ,PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ ,then ∠POQ is equal to :
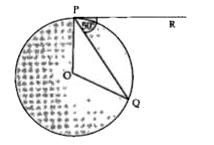
View SolutionIn the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
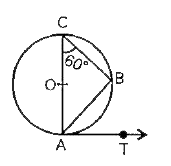
View SolutionIn the given figure, 0 is the centre of a circle and arc ABC subtends an angle of 130∘ at 0. AB is extended to P. Then, ∠PBC is equal to
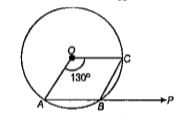
View Solution