ABC is a right triangle right angled at A. BCED,ACFG and ABMN are squares on the sides BC,CA and AB respectively. Line segments AX⊥DE meets BC at Y and DE at X. Join AD,AE also BF and CM
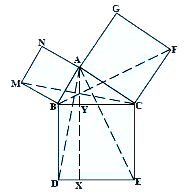
Show that
ar(BCED)=ar(ABMN)+ar(ACFG)
Can you write the result in words? This is a famous theorem of Pythagoras. You shall learn a simple proof in this theorem in class X.Solution in Telugu
Step by step video & image solution for ABC is a right triangle right angled at A. BCED,ACFG and ABMN are squares on the sides BC,CA and AB respectively. Line segments AX bot DE meets BC at Y and DE at X. Join AD,AE also BF and CM Show that ar(BCED)=ar(ABMN)+ar(ACFG) Can you write the result in words? This is a famous theorem of Pythagoras. You shall learn a simple proof in this theorem in class X. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) =2ar(MBC)
11:38View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) = ar(ABMN)
06:53View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: triangleFCB congtriangleACE
05:54View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = 2ar(FCB)
06:30View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = ar(ACFG)
06:44View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BCED) = ar(ABMN) + ar (ACFG)
07:05View SolutionABC is a right triangle right angled at A. BCED,ACFG and ABMN are squares on the sides BC,CA and AB respectively. Line segments AX⊥DE meets BC at Y and DE at X. Join AD,AE also BF and CM
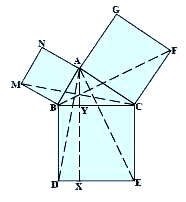
Show that
ΔFCB≅ΔACE04:04View Solution

