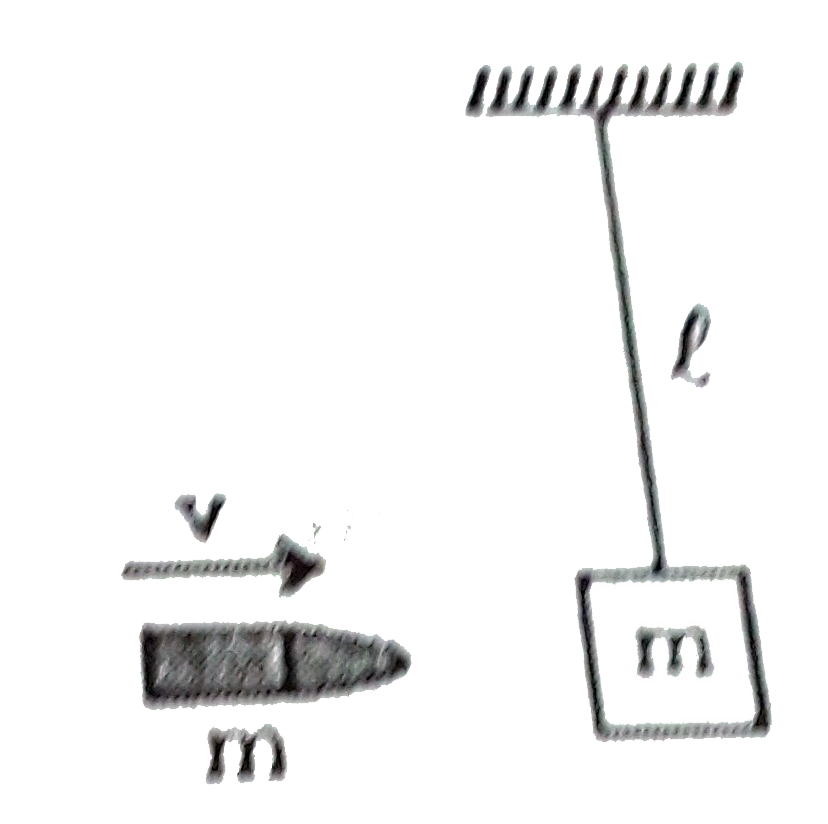
A bag of sand of mass M is suspended by a roap. A bullet of mass m. traveling with speed v gets. embedded in it. The loss of kinetic energy is

A

$M m v / (M + m)$

B

$(M + m) / M m v$

C

$\frac{M m v^{2}}{2 (M + m)}$

D

$\frac{2 (M + m)}{M v^{2}}$

Text Solution

Verified by Experts

The correct Answer is:C

Linear momentum is conserved.
$(M + m) v . = m v$
$∴ v . = \frac{m v}{M + m}$
$K E = \frac{1}{2} (M + m) v^{2}$
$∴ K E = \frac{1}{2} (M + m) \frac{m^{2} v^{2}}{{(M + m)}^{2}} = \frac{1}{2} \frac{m^{2} v^{2}}{(M + m)}$
Loss of KE = KE of bullet - KE of embedded bag
$= \frac{1}{2} m v^{2} - \frac{1}{2} \frac{m^{2} v^{2}}{M + m} = \frac{m M v^{2}}{2 (M + m)}$

|

Updated on:21/07/2023

Class 12 PHYSICS LAWS OF MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
A bag of sand of mass M is suspended by a string. A bullet of mass m is fired at it with velocity v and gets embedded into it. The loss of kinetic energy in this process is
A $\frac{1}{2} m v^{2}$
B $\frac{1}{2} m v^{2} \times \frac{1}{M + m}$
C $\frac{1}{2} m v^{2} \times \frac{M}{m}$
D $\frac{1}{2} m v^{2} (\frac{M}{M + m})$
Question 2 - Select One
A bag of sand of mass m is suspended by a rope. A bullet of mass $\frac{m}{20}$ is fired at it with a velocity vand gets embedded into it. The velocity of the bag finally is
A $\frac{v}{20} \times 21$
B $\frac{20 v}{21}$
C $\frac{v}{20}$
D $\frac{v}{21}$
Question 3 - Select One
A block of wood of mass $3 M$ is suspended by a string of length $\frac{10}{3} m$ . A bullet of mass $M$ hits it with a certain velocity and gets embedded in it. The block and the bullet swing to one side till the string makes $120^{\circ}$ with the initial position. the velocity of the bullet is $(g = 10 m s^{- 2})$ .
A $\frac{40}{\sqrt{3}} m s^{- 1}$
B $20 m s^{- 1}$
C $30 m s^{- 1}$
D $40 m s^{- 1}$ .

Recommended Questions

Home
Ask Doubt
Profile