R is the interatomic distance, a and b are positive constants, u denotes potential energy which is a function dependent on R as follows v=ar10−br5.The equilibrium distance between two atoms is
(b2a)15
(2ab)15
(b2a)110
(2ab)110
The correct Answer is:B
u=ar10−br5
dudr=−10ar11+5br6
dUdr=zero for equillibrium
∴0=−10ar11+5br6
∴2ar5=b∴r5=2ab
∴r=(2ab)1/5
Similar Questions
The potential energy (U) of diatomic molecule is a function dependent on r (interatomic distance )as U=αr10−βr5−3
Where αandβ are positive constants. The equilrium distance between two atoms will be (2αβ)ab where a=___
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View Solution
Knowledge Check
If r is the interatomic distance, a and b are positive constants, U denotes potential energy which is a function dependent on r as follows :
U=ar10−br5.
The equilibrium distance between two atoms isA(b2a)1/5B(2ab)1/5C(b2a)110D(2ab)110.If the potential energy is minimum for two atoms at r0=0.75Å. This is the equilibrium distance. Then,
Athe force is attractive at = r = 0.5 ÅBthe force is attractive at = r = 0.75 ÅCthe force is repulsive at r = 0.5 ÅDthe force is repulsive at r = 0.75 ÅThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.
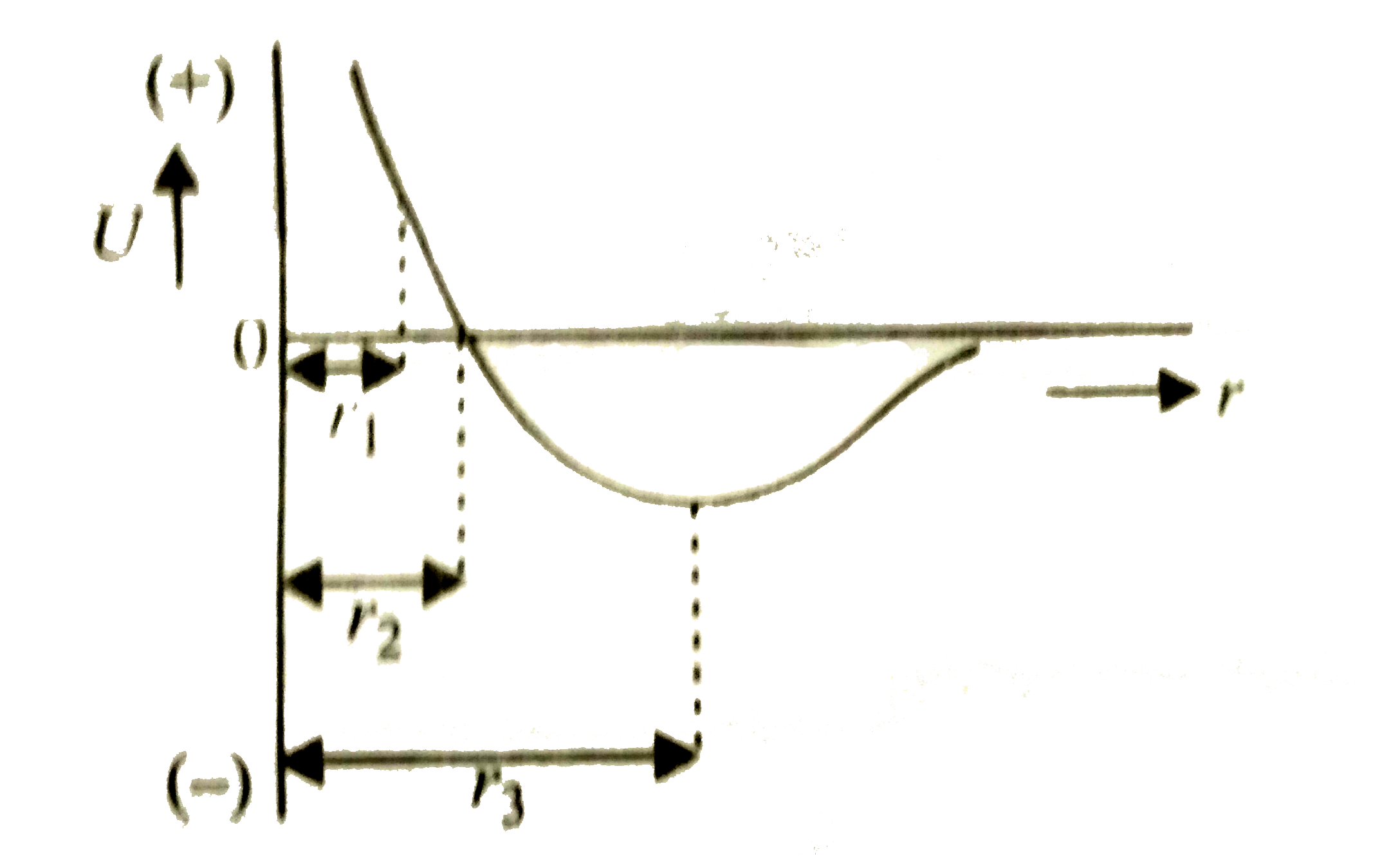
Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to r2.
2. At r=r1, the force between the atom is repulsive.
3. Forr>r2, the force between the atoms is attractive
Which of the above statements is true ?A1 onlyB2 onlyC3 onlyD2 and 3
Potential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
View SolutionThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.

Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to r2.
2. At r=r1, the force between the atom is repulsive.
. Forr>r2, the force between the atoms is attractive
Which of the above statements is true ?
View SolutionThe potential energy of a particle in a certain field has the form U=a/r2−b/r, where a and b are positive constants, r is the distance from the centre of the field. Find:
(a) the value of r0 corresponding to the equilibrium position of the particle, examine where this position is steady,
(b) the maximum magnitude of the attraction force, draw the plots U(r) and Fr(r) (the projections of the force on the radius vector r).
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View SolutionPotential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
View Solution
