Potential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
r=(6A11B)15
r=(11B6A)15
r=(6B11A)15
r=(11A6B)15
The correct Answer is:B
Step by step video & image solution for Potential energy in a field is given by U=-A/(r^6)+B/(r^11) then find the value of r for equilibrium position. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
If the potential energy between two molecules is given by U=−Ar6+Br12 , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View SolutionIf .10Pr =5040 , find the value of r
View SolutionIf potential energy is given by U=ar2−br. Then find out maximum force. (given a=2,b=4)
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionIn the given circuit, find the value of R :
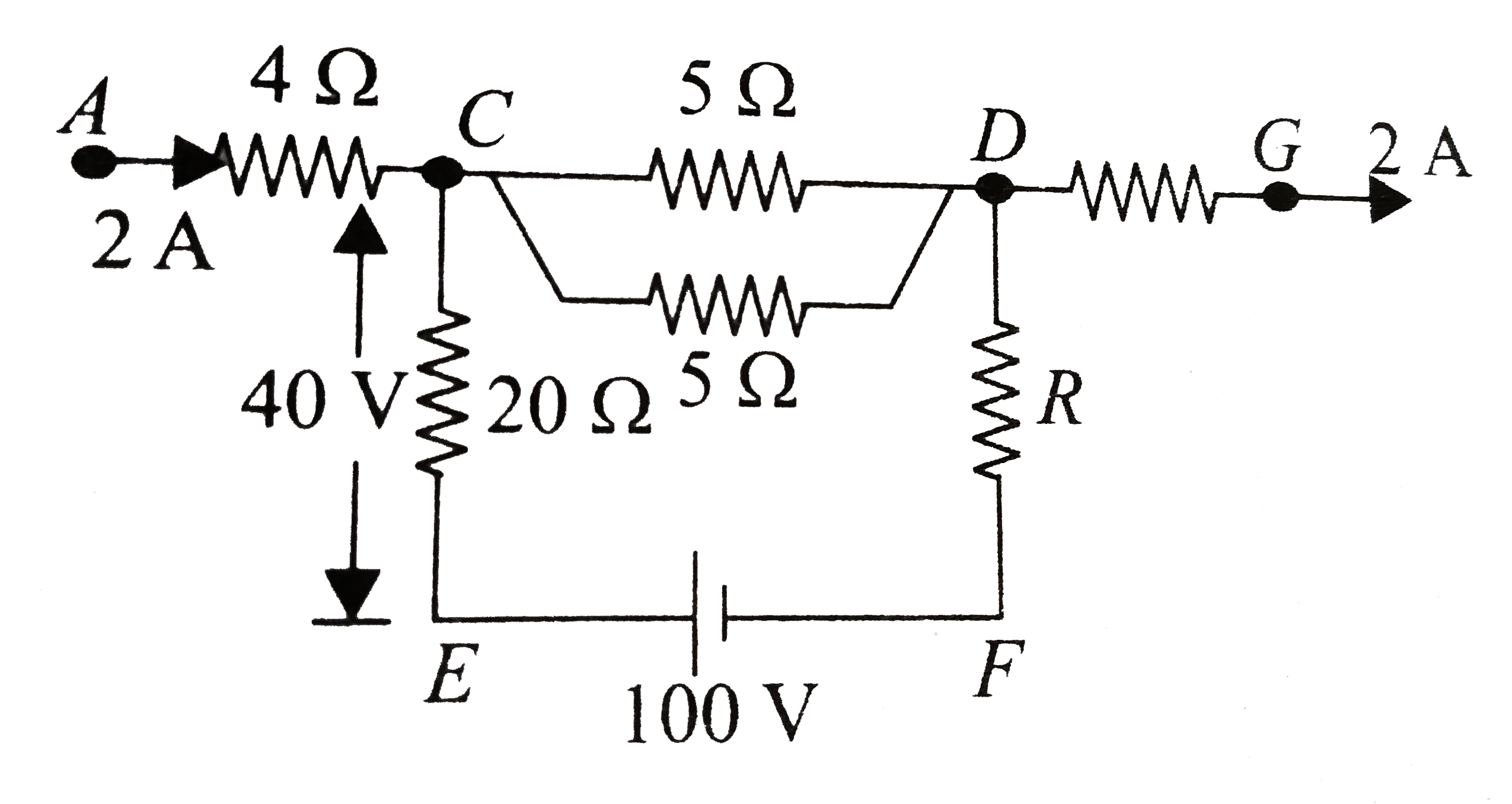 . View Solution
. View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle isView SolutionThe potential energy of a conservative force field is given by
U=ax2−bx
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.View SolutionPotential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
View Solution
