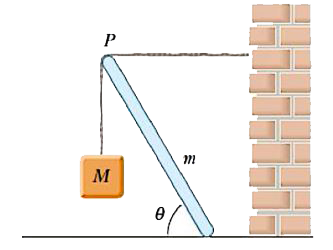
A uniform beam of mass m is
inclined at an angle θ to the
horizontal. Its upper end
produces a 90∘ bend in a very
rough rope tied to a wall, and
its lower end rests on a rough
floor(see figure). If the
coefficient of static friction
between the beam and the floor
is μ then the maximum value of
M is given by the expression
M≤m(2μ−cotθ)2(cotθ−μ)
M≤μm(1−3μ)
M≤m(2μ−tanθ)2(tanθ−μ)
M≤m(1−3μ)
The correct Answer is:A
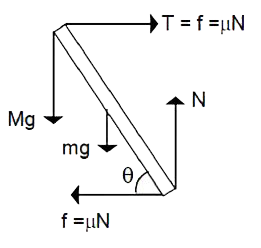
If the net torque about the lowest
point is set equal to zero, we get,
Mg L cos θ+mgL2cosθ−μN.Lsinθ=0
Where N=(M+m)g.
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 30BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 30EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 124 BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 124 EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 36BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 36EXERCISE - PHYSICS
30 Videos
Similar Questions
A uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
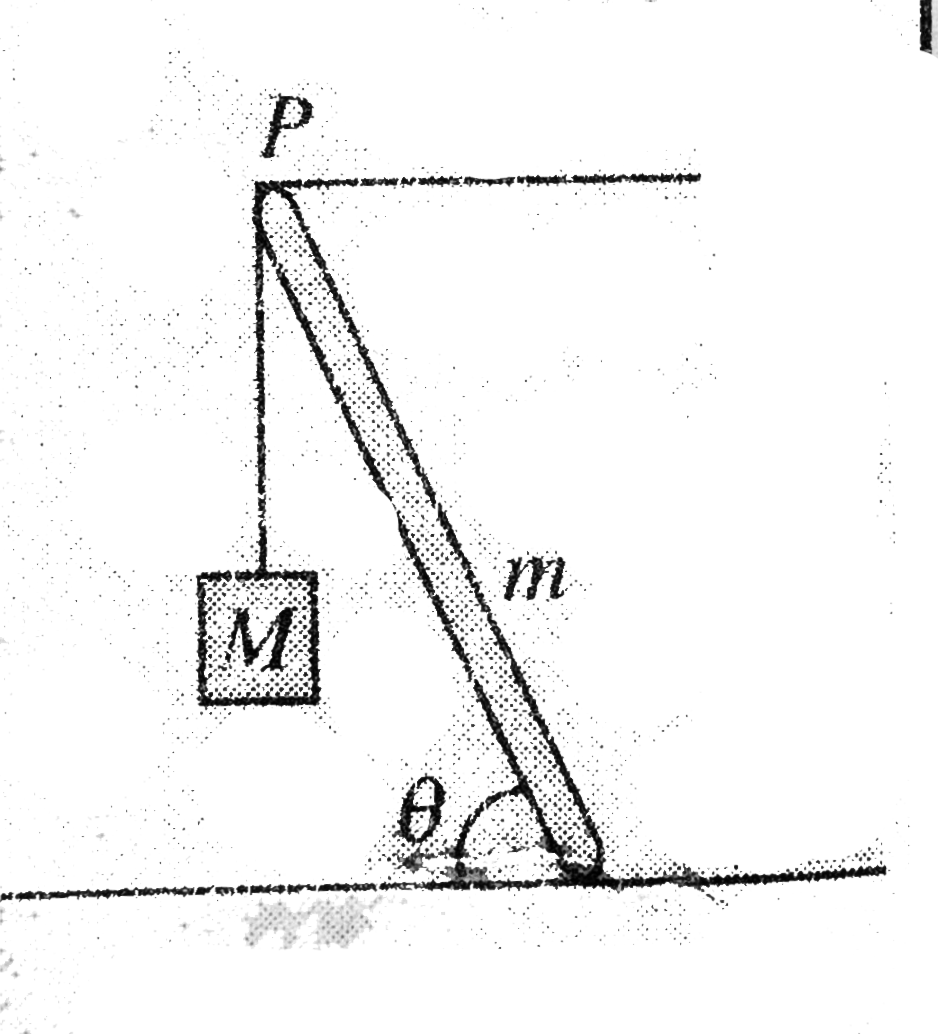 .
.
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
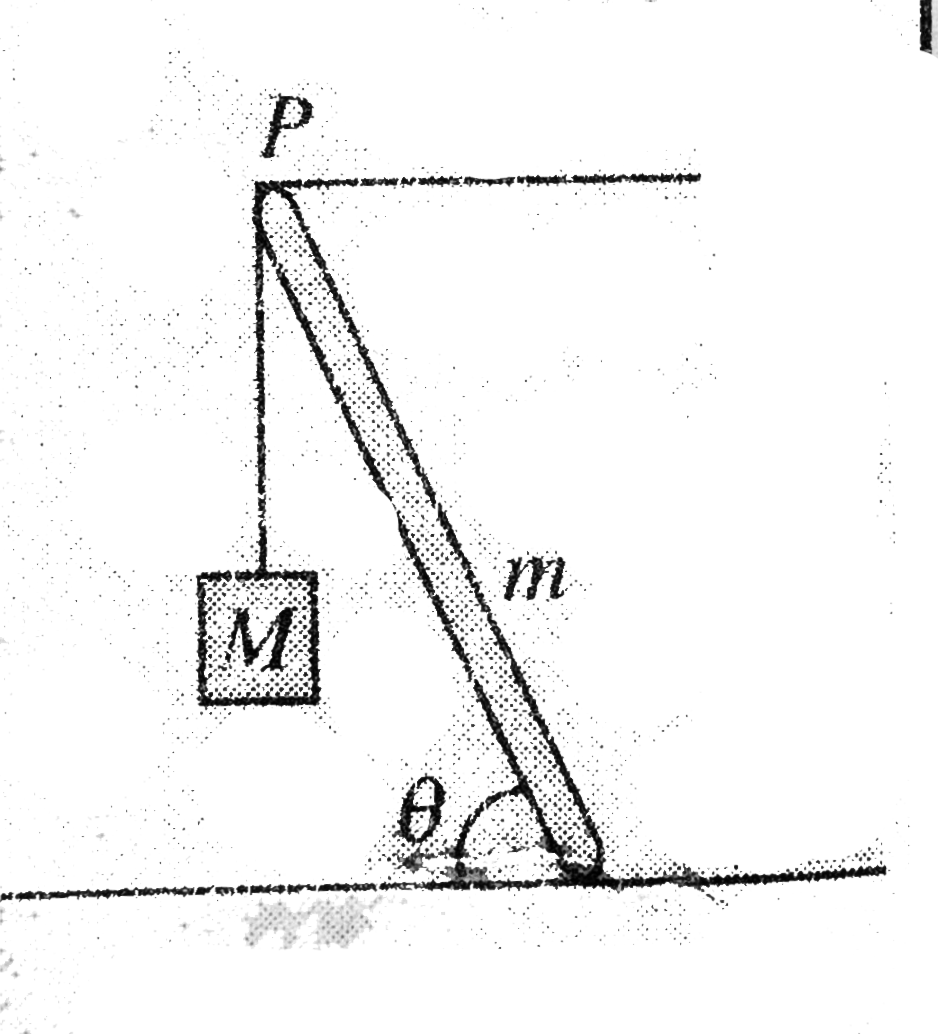 .
.
View Solution
Knowledge Check
A block of mass m is placed on a rough floor of a lift . The coefficient of friction between the block and the floor is μ. When the lift falls freely, the block is pulled horizontally on the floor. What is the force of friction -
AμmgBμmg/2C2μmgDNone of theseA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is μ
For what range of value of p , the block remain in static equilibrium ?

View SolutionA block of mass m is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is μ
For what range of value of p , the block remain in static equilibrium ?

View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
