As shown in the figure below, a rectangular block of mass M and length L is placed on a smooth table. A small cube of mass m with negligible length is placed on the left end of the block with horizontal initial velocity v sliding to the right. The coefficient of kinetic friction between the block and the cube is p, and the cube does not fall from the right end of the block. What is the displacement (in m ) of the rectangular block when the cube stops sliding on the rectangular block exactly at its right most end ? (Take m = 2 kg, M = 6 kg and L= 10 m)

The correct Answer is:2.50
Initially the velocity of the cube and rectangle block are v and 0 respectively. The kinetic frictin is fk=μmg and the acceleration on the cube and the block are
am=−μgandaM=μmgM
um=−μgt
uM=μmgtM
They will accelerate until they have the same velocity when the cube is at the right end, i.e..
v−μgt=μmgtM⇒(mM+1)μgt=v
⇒t=vμg(11+mM)
At this time the position of the cube and the right end of the block are :
xm=vt+12amt2=v2μg(11+mM)
−12v2μg(11+mM)2
=v2μg(11+mM)(1−12(11+mM))
xm=v2mg⎛⎜
⎜⎝12+mM(1+mM)2⎞⎟
⎟⎠
xm=L+12aMt2=L
+12mMv2μg(11+mM)2
If they coincide at time t
xm=xM
⇒v2μg1(1+mM)2(12+mM−12mM)=L
⇒v22μg=L(1+mM)⇒v
=√2μgL(1+mM)
The displacement of the block is
d=12aMt2=12mMv2μg(11+mm)2
=m2Mμg(11+mM)2×2μgL(1+mM)
d=LmM1+mM=(mm+M)L
=2×102+6=208=2.50m
Topper's Solved these Questions
Similar Questions
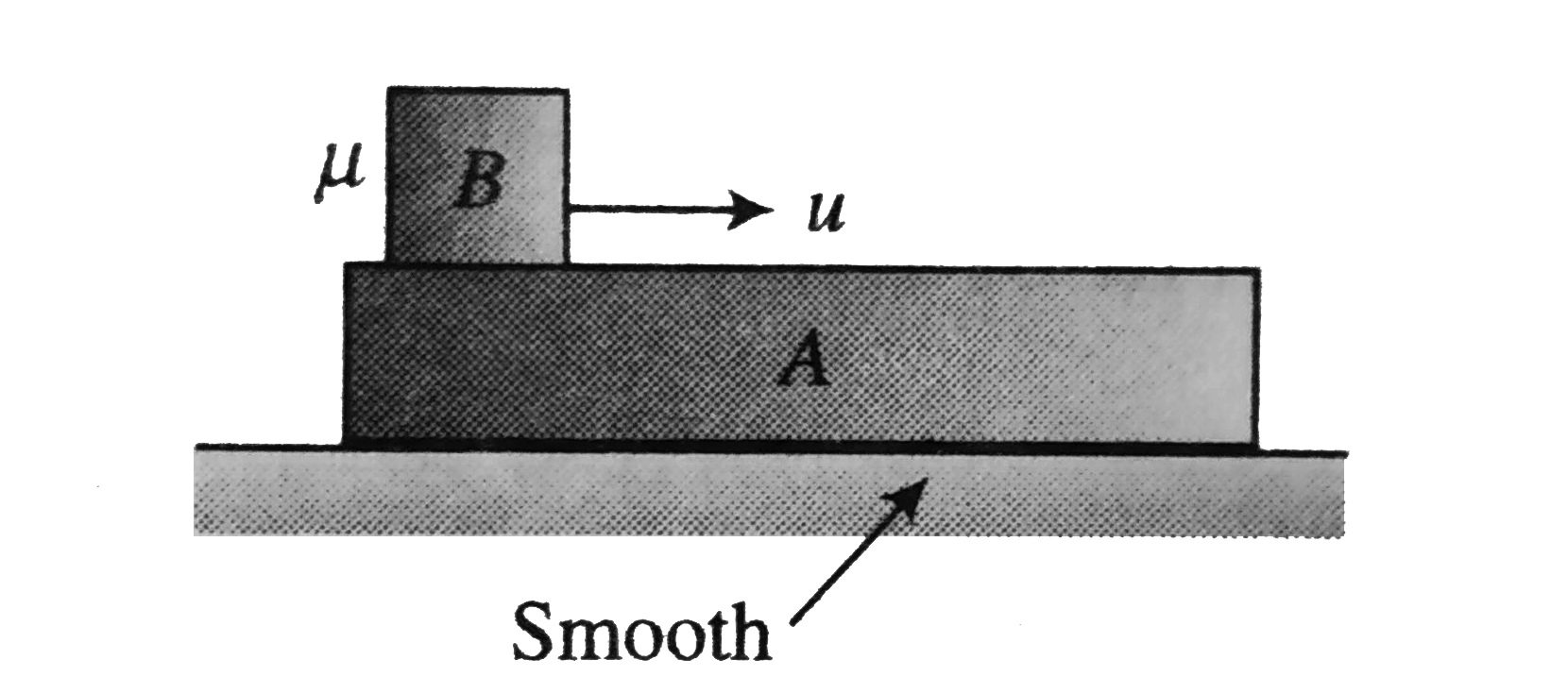
A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
View SolutionA block of mass m slides in right angled incliine through as shown in the figure . If the coefficient of kinetic friction between the block and the through is μk , find the acceleration of the block .

View Solution
Knowledge Check
A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
 A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.The block of mass m is in contact with a moving cart as shown in the figure.The coefficient of friction between the block and the cart is . The acceleration a of the cart that will prevent the block from falling is
 Aα≥gμBα<gμCα>mgμDα>gμm
Aα≥gμBα<gμCα>mgμDα>gμmA long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:
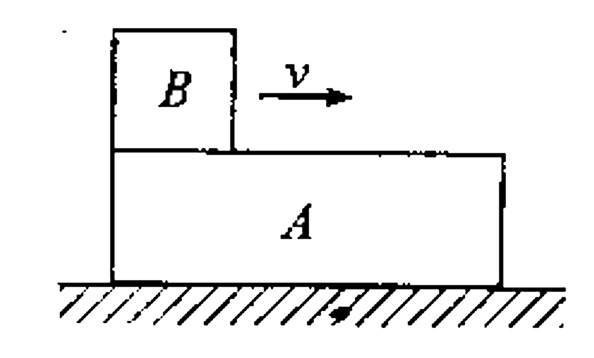 AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M/2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is μ then , the accelerations of blocks A and B before reaching a common velocity will be respectively

View Solution
