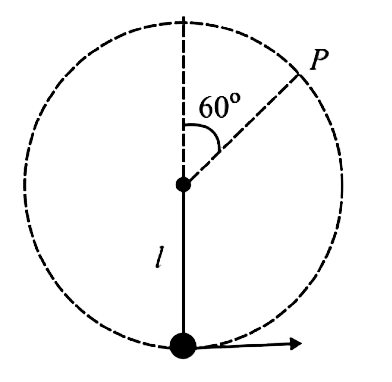
A particle attached to one end of a string of length l is given minimum velocity at lower most point to complete vertical circular motion. Net acceleration of the particle at the point P is g√αβ no where αandβ are lowest possible integers then fill the value of αβ
The correct Answer is:9.50
At point P,v=√2gl
⇒ac=vv2R=g√32
anet=√a2c+a2t
=g√192⇒α=19,β=2
Topper's Solved these Questions
Similar Questions
A particle is attached to a string and the other end of the string is attached to a fixed support. In order to just complete the vertical circular motion, what should be the ratio of the kinetic energy of the particle at its highest point of that at its highest point to that at its lowest point?
View SolutionA particle is attached to a string and the other end of the string is attached to a fixed support. In order to just complete the vertical circular motion, what should be the ratio of the kinetic energy of the particle at its highest point of that at its highest point to that at its lowest point?
View Solution
Knowledge Check
The maximum velocity and maximum acceleration of a particle per for ming a linear SHM are αandβ respectively. Then path length of the particle is
Aα2βBβ2α2C2α2βD2βα2A mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)Aglancing angleB3gC4gD6gA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
A√5glB√5gl(cosα+1)C√5gl/tanαD√5glsinα
In a park there are three concentric circular running tracks. Radius of 2 nd track is double of the first and of 3rd track is triple of the first. Three runners are running on these tracks with constant speed. When the runner in the first track completes one round, the runner in 2nd has completed half round and the runner in third track has completed quarter round. If the accelerations of the runners are in ratio α:β:γ, where α,β and γ are least integers, then find the value of α+β+γ9.
View SolutionA mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)
View SolutionA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View Solution
