As indicated in the following figure a circular conducting wire is connected in such a way that current flows through two arcs of lengths L1 and L2 respectively. Calculate the magnitude of magnetic induction at the centre of the coil.
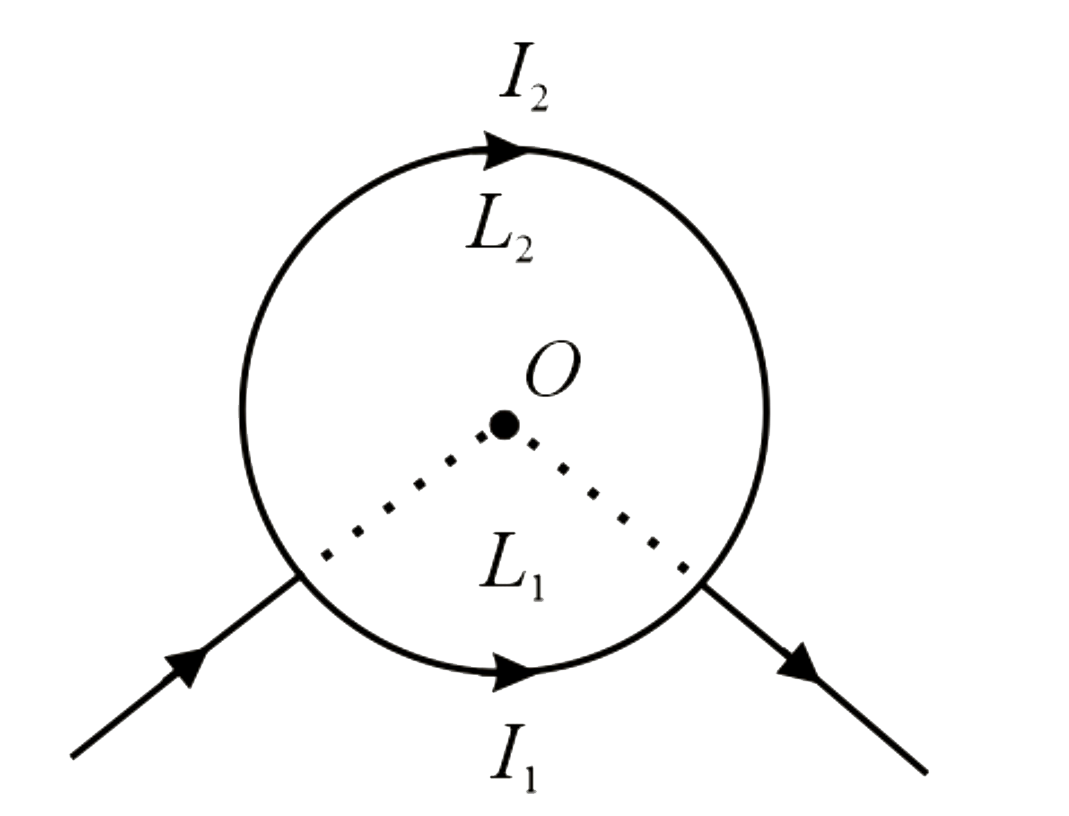
zero
μ0πI2r
μ0I2r
μ0I2π
The correct Answer is:A
By breaking value of current in both upper and lower part, we can see that current will be arranged in such a manner that both parts will produce equal magnitude of magnetic fiedl (as both upper and lower part have to maintian same potential difference)
Mathamaticaly
Assume θ to be the angle subtended by the arc L1
360∘−θ will be the angle subtended by the arc L2
We know that the resistance is proportional to the length and hence in the case of circular arc, proportional to the angle subtended by the arc.
By V=IR, we have
I∝IR∝1θ (since the potential difference across them is same)
Now, magnetic field due to circular arc is B=μ0Iθ4πr
Clearly B∝θ
But the product of I.θ is constant in our case
So B1=B2
By applying right hand thumb rule on both the parts of the circle we can see that magnetic field is in opposite direction at the centre. Thus net magnetic field at the centre will be equal to zero.
Topper's Solved these Questions
Similar Questions
The current through a circular coil appears to be flowing in clock-wise direction for an observer. The magnetic induction at the centre of the coil is:
View SolutionA conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View Solution
Knowledge Check
A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πLA current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
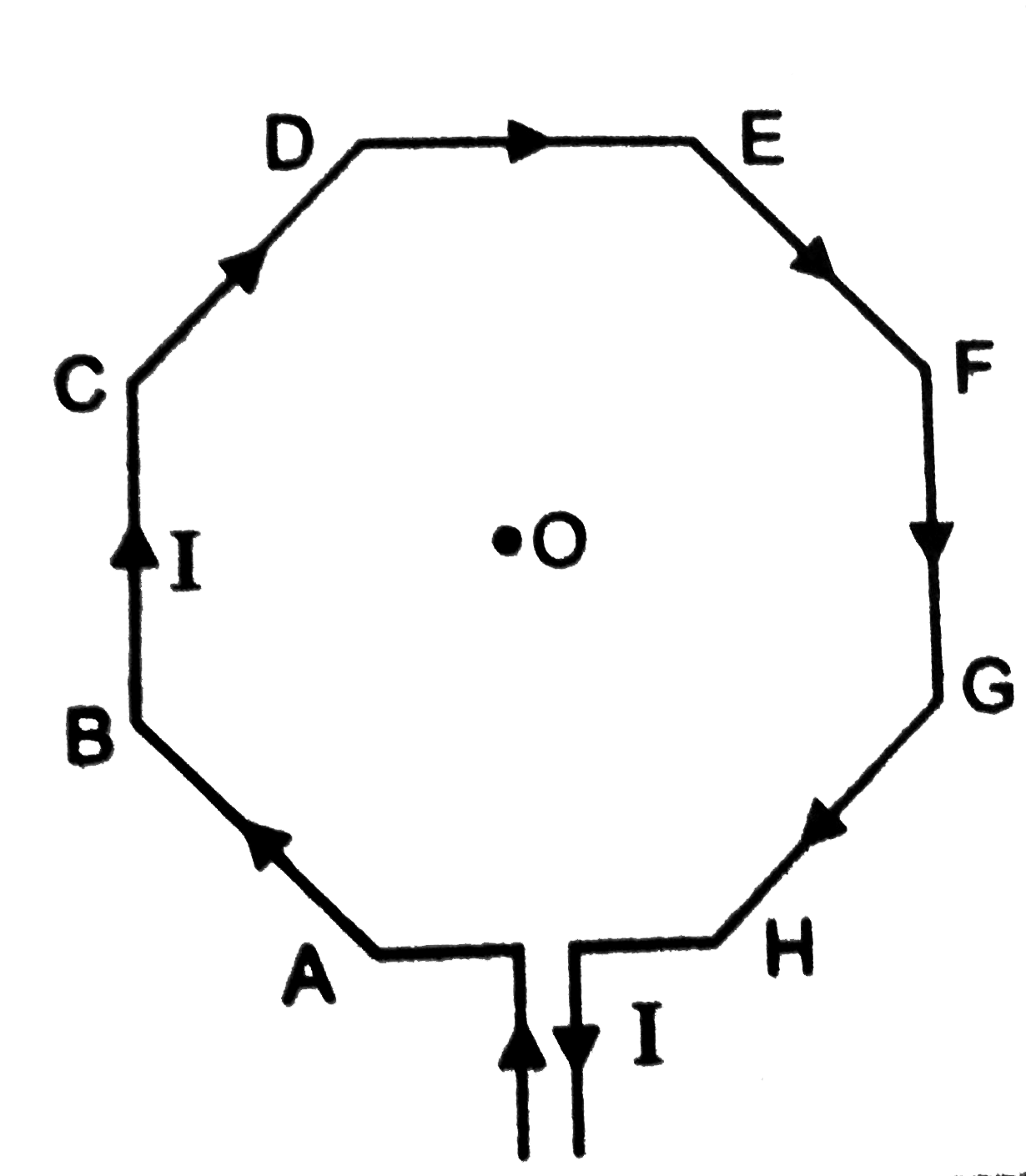 A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πaTwo circular coils are made of two identical wires of same length and carry same current. If the number of turns of the two coils are 4 and 2, then the ratio of magnetic induction at the centres will be
A2:1B1:2C1:1D4:1
A system consists of two coaxial current carrying circular loops as shown in Fig. The self inductance of loop 1 is L1 and self inductance of loop 2 is L2. Magnitude of mutual inductance is M. If at any instant current flowing through loop 1 and loop 2 are i1andi2 respectively, then total magnetic energy of the system is
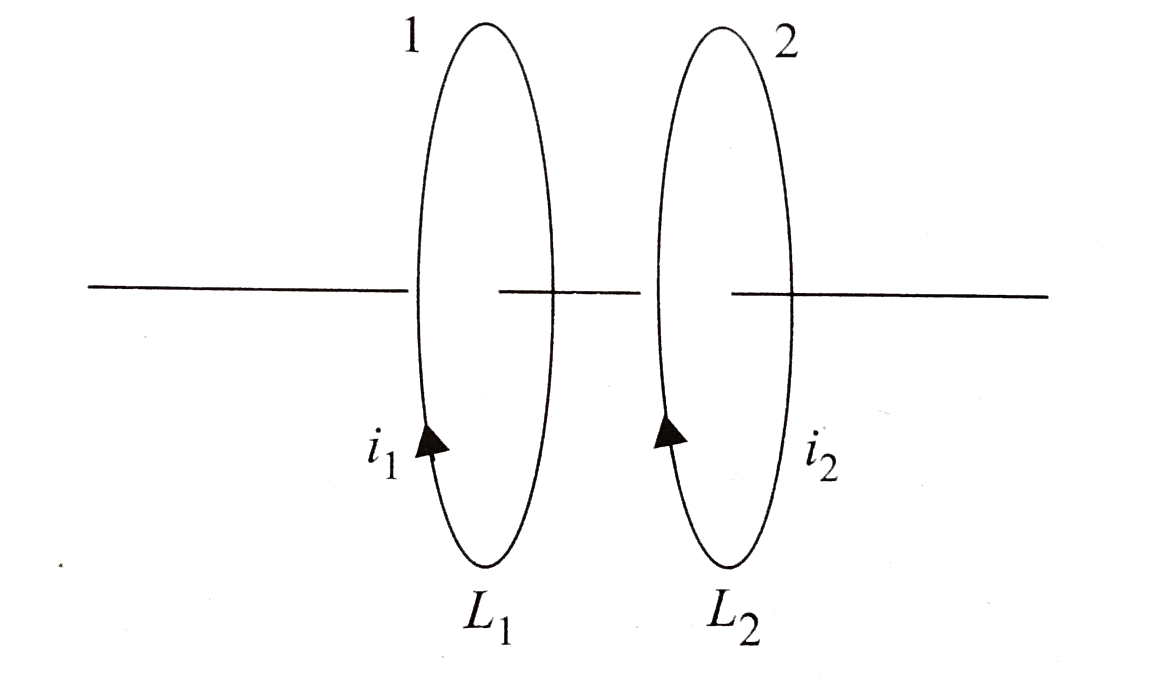
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
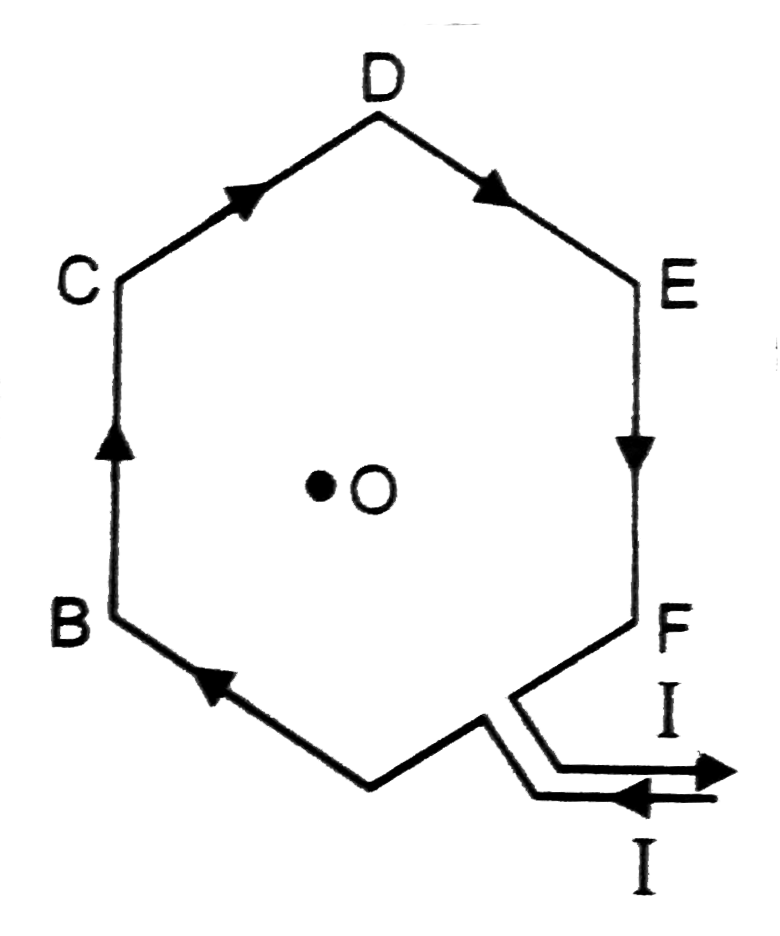
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be

View SolutionA conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
View SolutionA system consists of two coaxial current carrying circular loops as shown in Fig. The self inductance of loop 1 is L1 and self inductance of loop 2 is L2. Magnitude of mutual inductance is M. If at any instant current flowing through loop 1 and loop 2 are i1andi2 respectively, then total magnetic energy of the system is
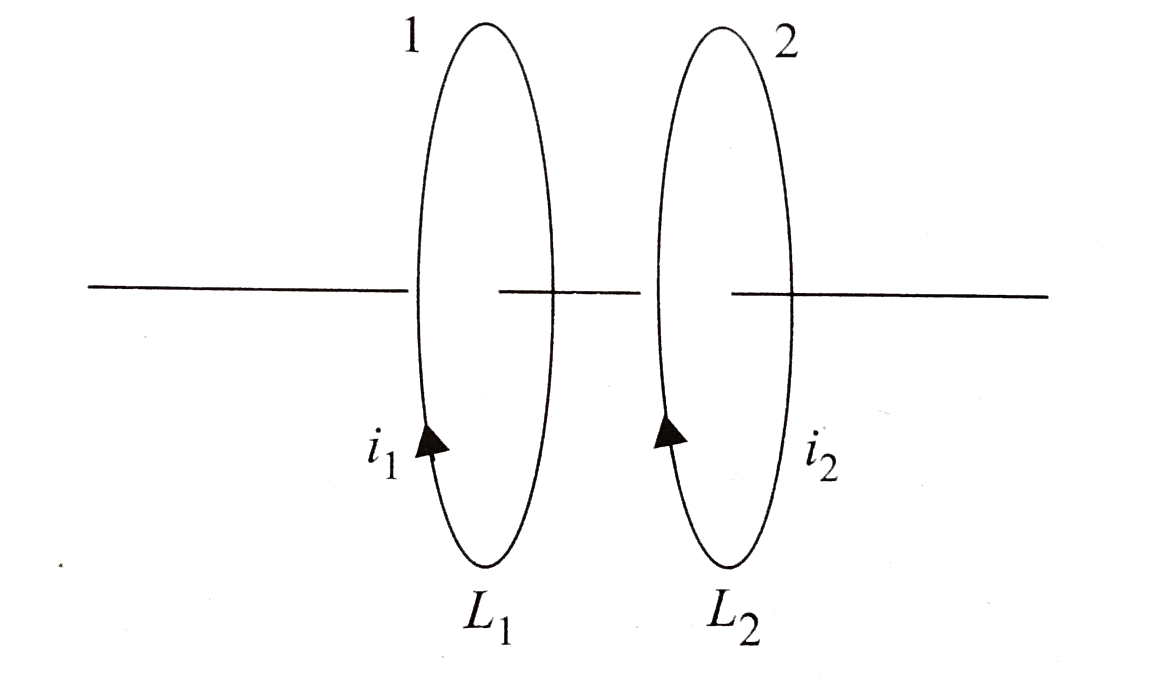
View Solution
