A plano-convex lens with R.I. μ1 and power P1 is placed in contact with a plano concave lens with R.I. μ2 and power P2
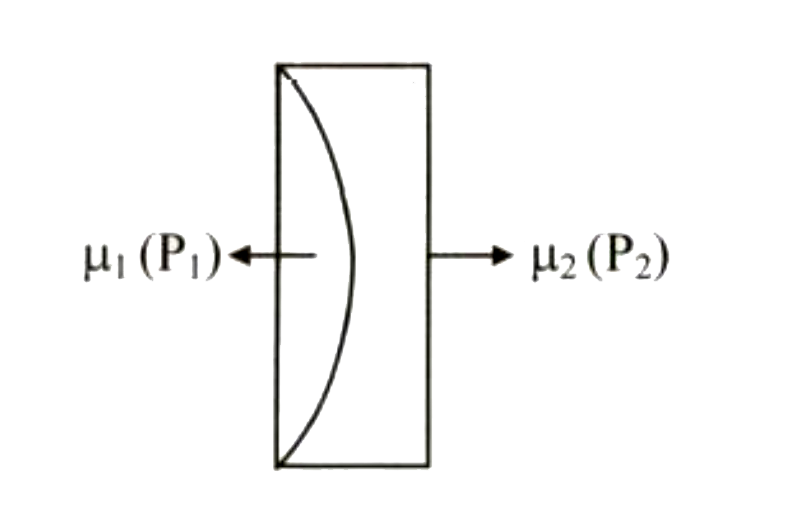
Let both lenses have same radius of curvature R each and P2=2P1. Then the refractive indices are related to each other as μ1+μ22=n. What is the value of n?
The correct Answer is:01.50
From lens maker.s equation
P=1f=(μ−1)(1R1−1R2)
For plano convex lens
R1=∞,R2=−R
∴P1=(μ1−1)(1∞−1−R)
=(μ−1)R
For plano concave lens
R1=−R,R2=∞
∴P2=(μ2−1)(1−R−1∞)
=−(μ2−1)R
Given that
P2=2P1
∴−(μ2−1)R=2(μ1−1)R
∴−μ2+1=2μ1−2
∴2μ1+μ2=3
∴μ+μ22=1.5
Topper's Solved these Questions
Similar Questions
A plano convex lens of refractive index μ1 and focal length f1 is kept in contact with another plano concave lens of refractive index μ2 and focal length f2. If the radius of curvature of their spherical faces is R each and f1=2f2, then μ1 and μ2 are related as :
View SolutionA plano convex lens of refractive index μ1 and focal length f1 is kept in contact with another plano concave lens of refractive index μ2 and focal length f2. If the radius of curvature of their spherical faces is R each and f1=2f2, then μ1 and μ2 are related as :
View Solution
Knowledge Check
A Plane convex lens of refractive index μ1 and focal length f1 is kept in contact with another plane concave lens of refractive index μ2 and focal length f2 If the radius of curvature of their spherical faces is R each and f1=3f2 then μ1 and μ2 are related as:
Aμ1+μ2=3B3μ1−2μ1=1C3μ2−μ1=1D3μ1−μ2=2The power of a double convex lens of radius of curvature R each is Y. The power of a plano convex lens of same material and of radius of curvature 2R is
AY4BY2C2YD4YIf the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
Af=R2(μ+1)Bf=2R(μ+1)Cf=2Rμ+1Df=R2(μ−1)
The figure below shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. Another thin lens of refractive index μ3 has same radius of curvature R on the two surface between the plano-convex and plano-concae lenses that the plane surfaces are parallel to each other. Find the focal length of the combination.
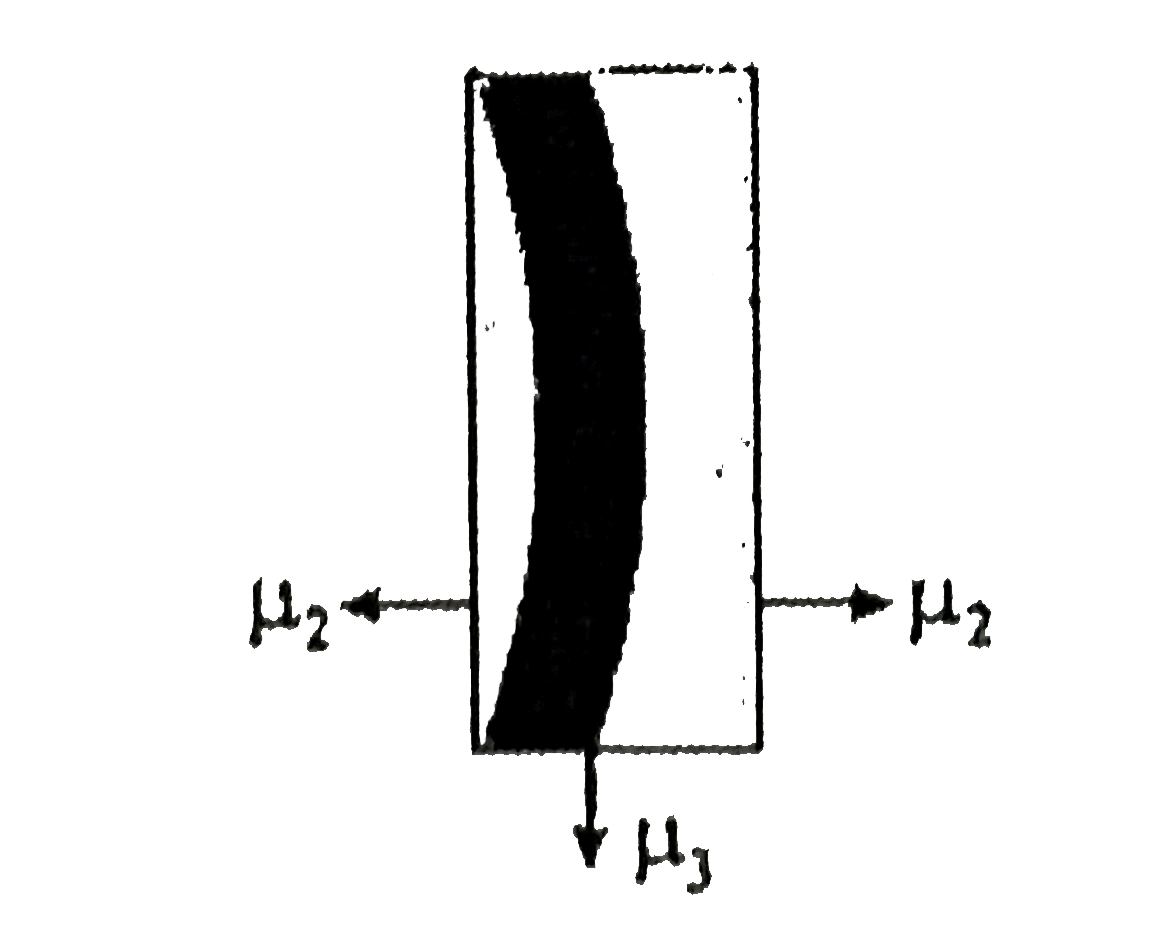
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionIf the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
View SolutionA plano-convex lens (focal length f2, refractive indexμ2, radius of curvature R) fits exactly into a plano-concave lens (focal lengthf1 refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View Solution
