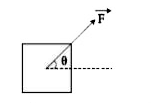
A block of mass (m) slides along the track with kinetic friction μ. (A) man pulls the block through a rope which makes an angle θ with the horizontal as shown in the figure. The block moves with constant speed v. Power delivered by man is
 .
.
Tv
Tvcosθ
(Tcosθ−μmg)v
zero
The correct Answer is:B
Instantaneous power is given as P=Fvcosϕ
Here, angle ϕ between tension and velocity is θ
So, P=Tvcosθ
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 47BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 47EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 46BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 46EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 48BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 48EXERCISE - PHYSICS
29 Videos
Similar Questions
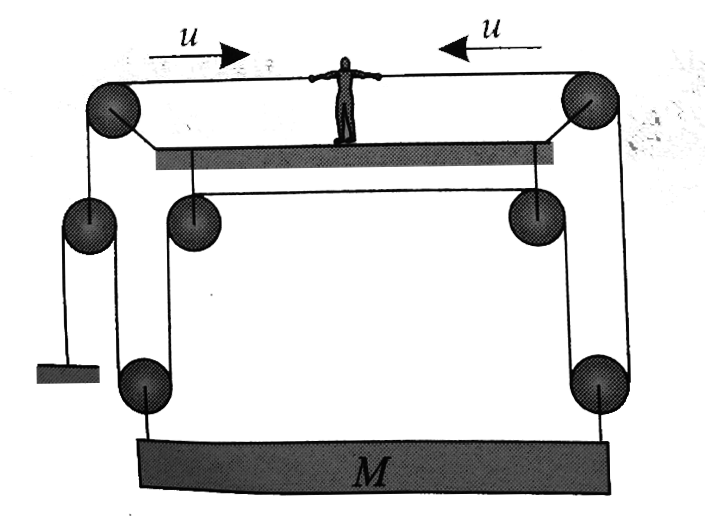
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
View SolutionA block of mass m slides along a floor while a force of magnitude F is applied to it at an angle θ as shown in figure. The coefficient of kinetic friction is μr. Then, the block's acceleration 'a' is given by:
(g is acceleration due to gravity)
View Solution
Knowledge Check
A block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionA block of mass M is at rest on a rough horizontal surface. The coefficient of friction between the block and the surface is μ. A force F = Mg acting at an angle θ with the vertical side of the block pulls it. In which of the following cases, the block can be pulled along the surface?
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force P is applied at one end of rope. The force which the rope exerts on the block is:
View Solution
