Four monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
The correct Answer is:06.00
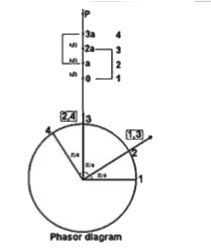
λ=λ8
ϕ between 1 and 3 =2πλ×λ4=π2
ϕ between 2 and 4 =π2
Intensity because of 1 and 3, 2 and 4
=I1+I2+2√I1I2cosϕ=I0+I0+2√I0I0cos(π/2)=2I0
Now phase difference between resultant of 1 and 3, 2 and 4 π4
∴I=I1+I2+2√I1,√I2cosd
=2I0+2I0+2√2×√2I0×1√2
4I0+2√2I0
(4I0+2√2)I0
=6.8I0
∴[n]=6
Topper's Solved these Questions
Similar Questions
Four monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View SolutionTwo incoherent sources of light emitting light of intensity I0 and 3I0 interfere in a medium. Then the resultant intensity at any point will be
View Solution
Knowledge Check

In the figure the intensity of waves arriving at D from two coherent sources S1 and S2 is I0 The wavelength of the wave is λ=4m. Resultant intensity at D will be:A4I0BI0C2I0DzeroIn the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be
 A4l0Bl0C2l0Dzero
A4l0Bl0C2l0DzeroThere is an equilateral triangle ABC. Two monochromatic and coherent sources of light are placed at points A and B. Intensity of light from both the sources reaching the point C is same and equal to 2W/m2. Resultant intensity of light at point C
Ais 8W/m2Bis 4W/m2Cis zeroDcannot be determined with the given information
Two incoherent sources of light emitting light of intensity I0 and 3I0 interfere in a medium. Calculate, the resultant intensity at any point.
View SolutionThe intensity of interference waves in an interference pattern is same as I0. The resultant intensity at the point of observation will be
View Solution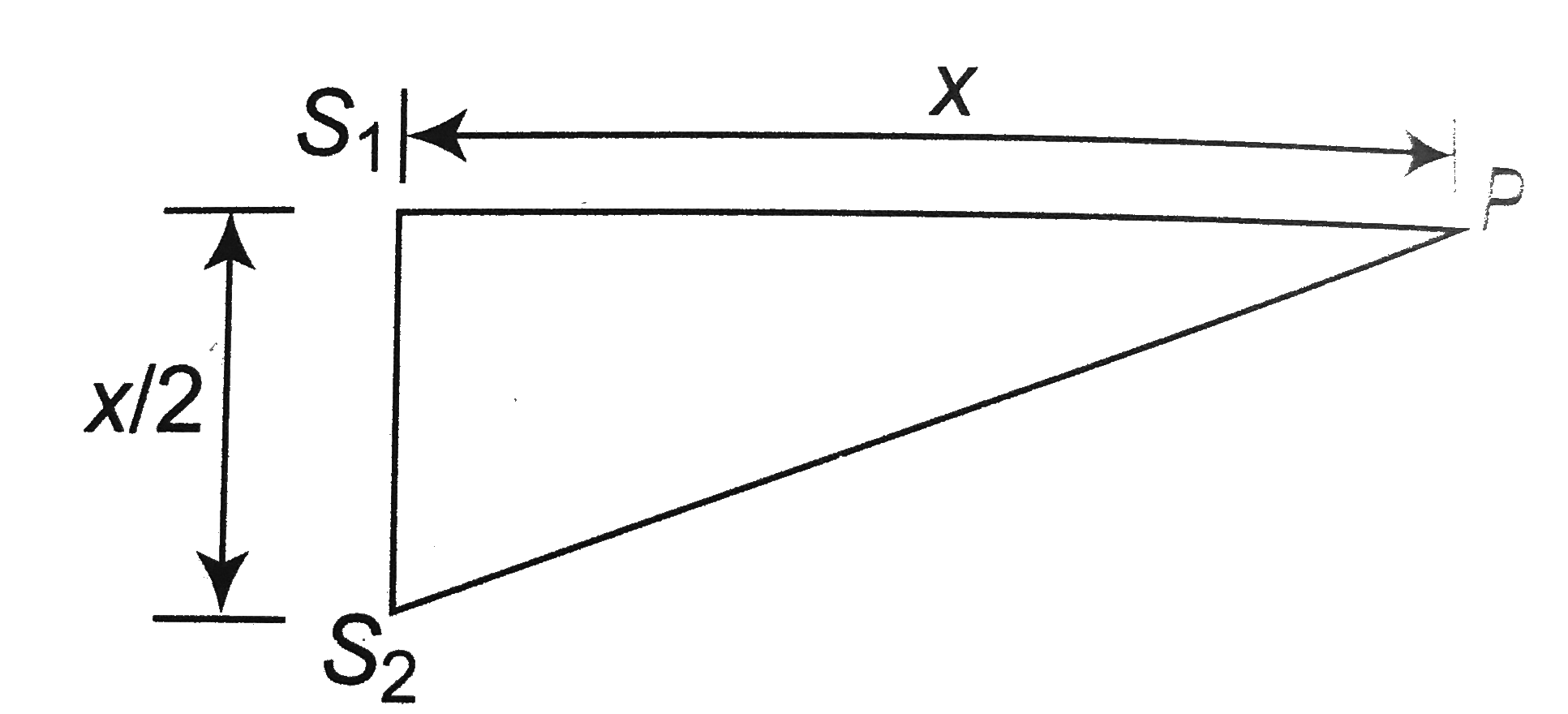
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View SolutionLight from two coherent sources of the same amplitude A and wavelength λ illuminates the screen. The intensity of the central maximum is I0. If the sources were incoherent, the intensity at the same point will be
View SolutionLight from two coherent sources of the same amplitude A and wavelength λ illuminates the screen. The intensity of the central maximum is I0. If the sources were incoherent, the intensity at the same point will be
View Solution