A man of 80 kg fastns a rope to a mass of 120kg, and passes the rope over a smooth pulley. In order to raise it up he climbs the riope with acceleration 3g2 relative to the rope. Calculate the tension in the rope in N. (Take g=10m/s2)
The correct Answer is:1680
To solve the problem of finding the tension in the rope when a man of 80 kg climbs a rope attached to a mass of 120 kg with an acceleration of 3g2 relative to the rope, we can follow these steps:
Step 1: Understand the System
We have a man of mass m1=80kg climbing a rope attached to a mass m2=120kg over a smooth pulley. The acceleration of the man relative to the rope is given as arel=3g2.
Step 2: Define the Acceleration
Let g=10m/s2. The weight of the man is:
W1=m1⋅g=80⋅10=800N
The weight of the block is:
W2=m2⋅g=120⋅10=1200N
Step 3: Determine the Acceleration of the Man
The acceleration of the man with respect to the ground ap can be expressed as:
ap=arel−a
where a is the acceleration of the block. Since the man is climbing up, the block will move down with acceleration a.
Step 4: Write the Equation for the Man
Using Newton's second law for the man:
T−W1=m1⋅ap
Substituting ap:
T−800=80(3g2−a)
Substituting g=10:
T−800=80(15−a)
T−800=1200−80a(Equation 1)
Step 5: Write the Equation for the Block
Using Newton's second law for the block:
T−W2=−m2⋅a
This gives:
T−1200=−120a(Equation 2)
Step 6: Solve the Equations
Now we have two equations:
1. T−800=1200−80a
2. T−1200=−120a
From Equation 2, we can express T:
T=1200−120a
Substituting T from Equation 2 into Equation 1:
1200−120a−800=1200−80a
Simplifying:
400−120a=1200−80a
Rearranging gives:
400=1200+40a
40a=400−1200
40a=−800
a=−20m/s2
Step 7: Substitute Back to Find Tension
Now substitute a back into the equation for T:
T=1200−120(−20)
T=1200+2400
T=3600N
Final Answer
The tension in the rope is:
3600N
We have a man of mass m1=80kg climbing a rope attached to a mass m2=120kg over a smooth pulley. The acceleration of the man relative to the rope is given as arel=3g2.
Let g=10m/s2. The weight of the man is:
W1=m1⋅g=80⋅10=800N
The weight of the block is:
W2=m2⋅g=120⋅10=1200N
The acceleration of the man with respect to the ground ap can be expressed as:
ap=arel−a
where a is the acceleration of the block. Since the man is climbing up, the block will move down with acceleration a.
Using Newton's second law for the man:
T−W1=m1⋅ap
Substituting ap:
T−800=80(3g2−a)
Substituting g=10:
T−800=80(15−a)
T−800=1200−80a(Equation 1)
Using Newton's second law for the block:
T−W2=−m2⋅a
This gives:
T−1200=−120a(Equation 2)
Now we have two equations:
1. T−800=1200−80a
2. T−1200=−120a
T=1200−120a
1200−120a−800=1200−80a
Simplifying:
400−120a=1200−80a
Rearranging gives:
400=1200+40a
40a=400−1200
40a=−800
a=−20m/s2
Now substitute a back into the equation for T:
T=1200−120(−20)
T=1200+2400
T=3600N
The tension in the rope is:
3600N
Topper's Solved these Questions
Similar Questions
To raise a weight which is half as much again as his weight a man fastens a rope to it and passes over a smooth pulley, he then climbs up the rope with an acceleration 6g7 relative to the rope. Show that the weight rises with acceleration 87, and find the tension of the rope.
View SolutionTension in the rope at the rigid support is (g=10m/s2)
View Solution
Knowledge Check
In order to raise a mass of 100kg a of mass 60kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is: Take g=10m/s2
A1432NB928NC1219ND642NIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is (take g=10ms−2)
 A48758NB48752NC48754ND48756N
A48758NB48752NC48754ND48756NIn order to raise a mass of 100kg a man of mass 60kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is: Take g=10m/s2
A1432NB928NC1218ND642N
A boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
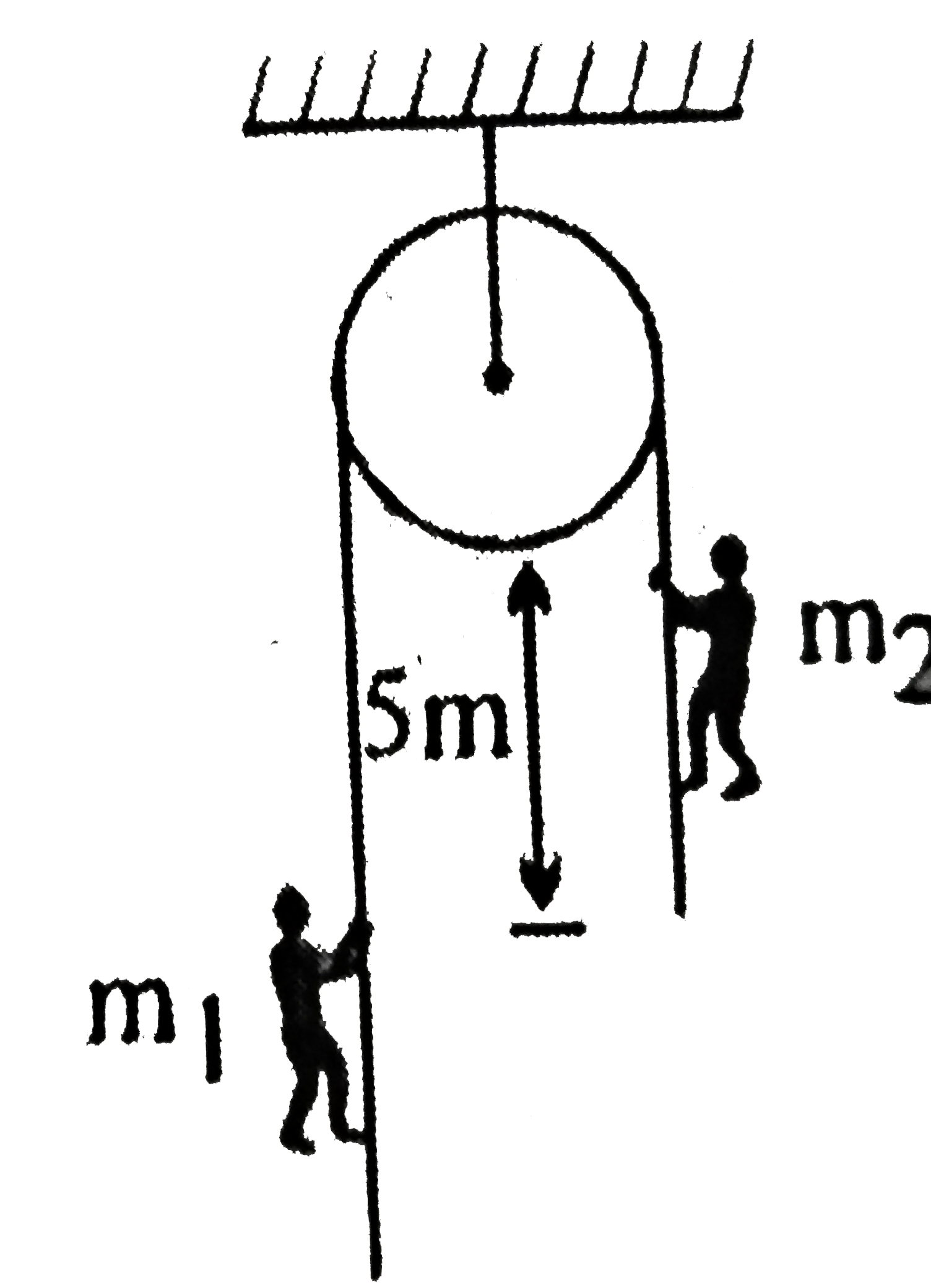
View SolutionA person of 70kg mass is lifted vertically upwards by a helicopter with the help of a rope hanging from it.If the helicopter is rising up with an acceleration 4ms2 the tension in the rope is (g=10ms2
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
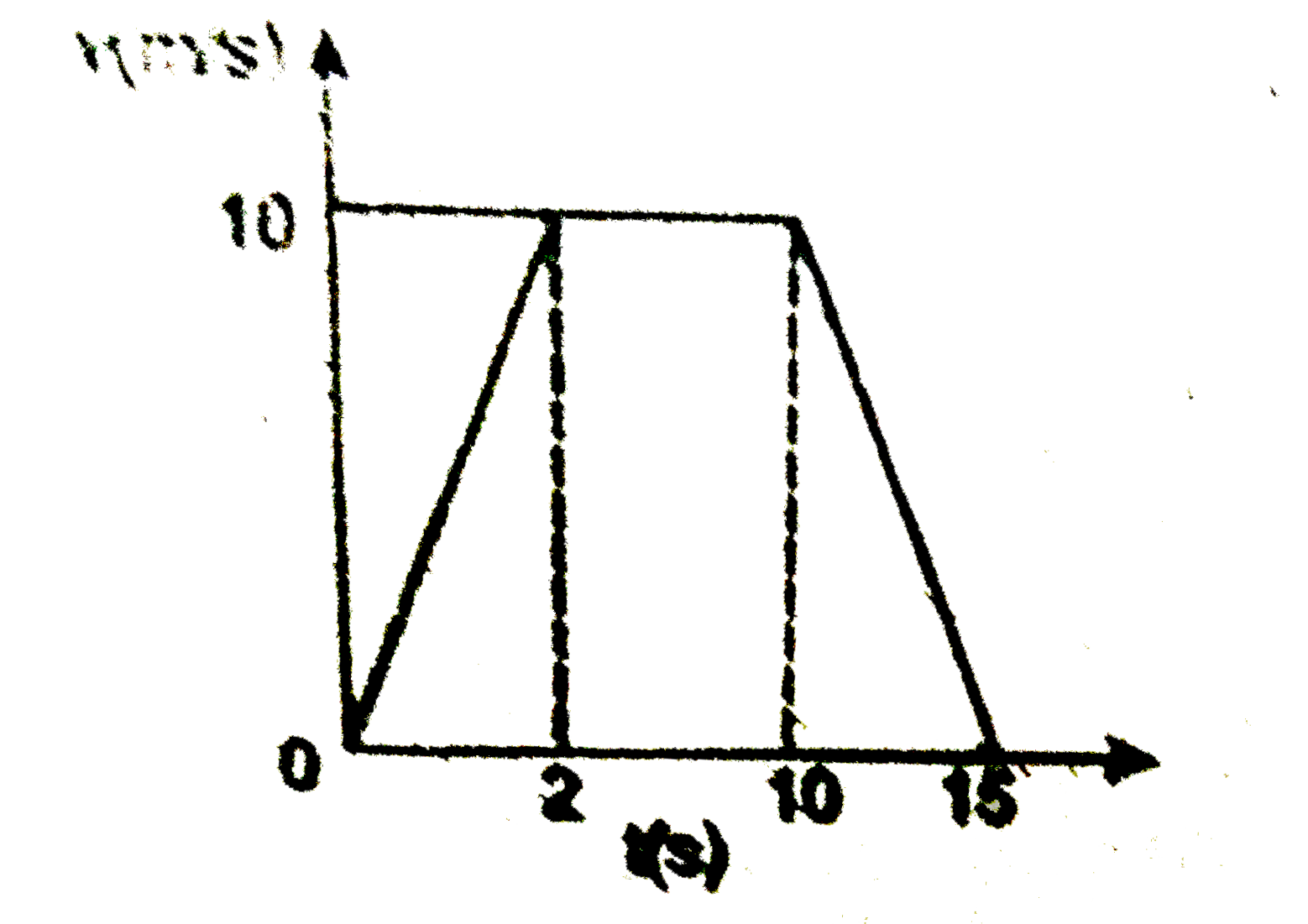
View SolutionA monkey of mass 40 kg climbs on a massless rope of breaking strength 600 N. The rope will break if the monkey. (Take g=10m/s2)
View Solution
