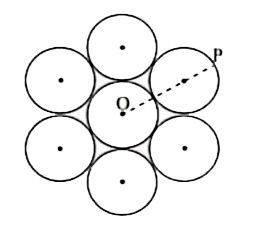
Seven identical circular rings of mass 8 g and radius 2 cmare welded symmetricallyas depicted in the adjoinig figure. The moment of inertia of the given configuration about an axis that passes through P and is perpendicular to the plane is _______×10−5kgm2
The correct Answer is:30.08
M.I. about origin O
IO=MR2+6[MR2+M(2R)2]
∴IO=MR2+30MR2
IO=32MR2
Using parallel axes theorem,
M.I. about the point P will be
IP=IO+7M(3R)2
IP=31MR2+63MR2
IP=94MR2=94×8×10−3
×(2×10−2)2
∴IP=30.08×10−5kgm2
Topper's Solved these Questions
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionSeven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

View Solution
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2
Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
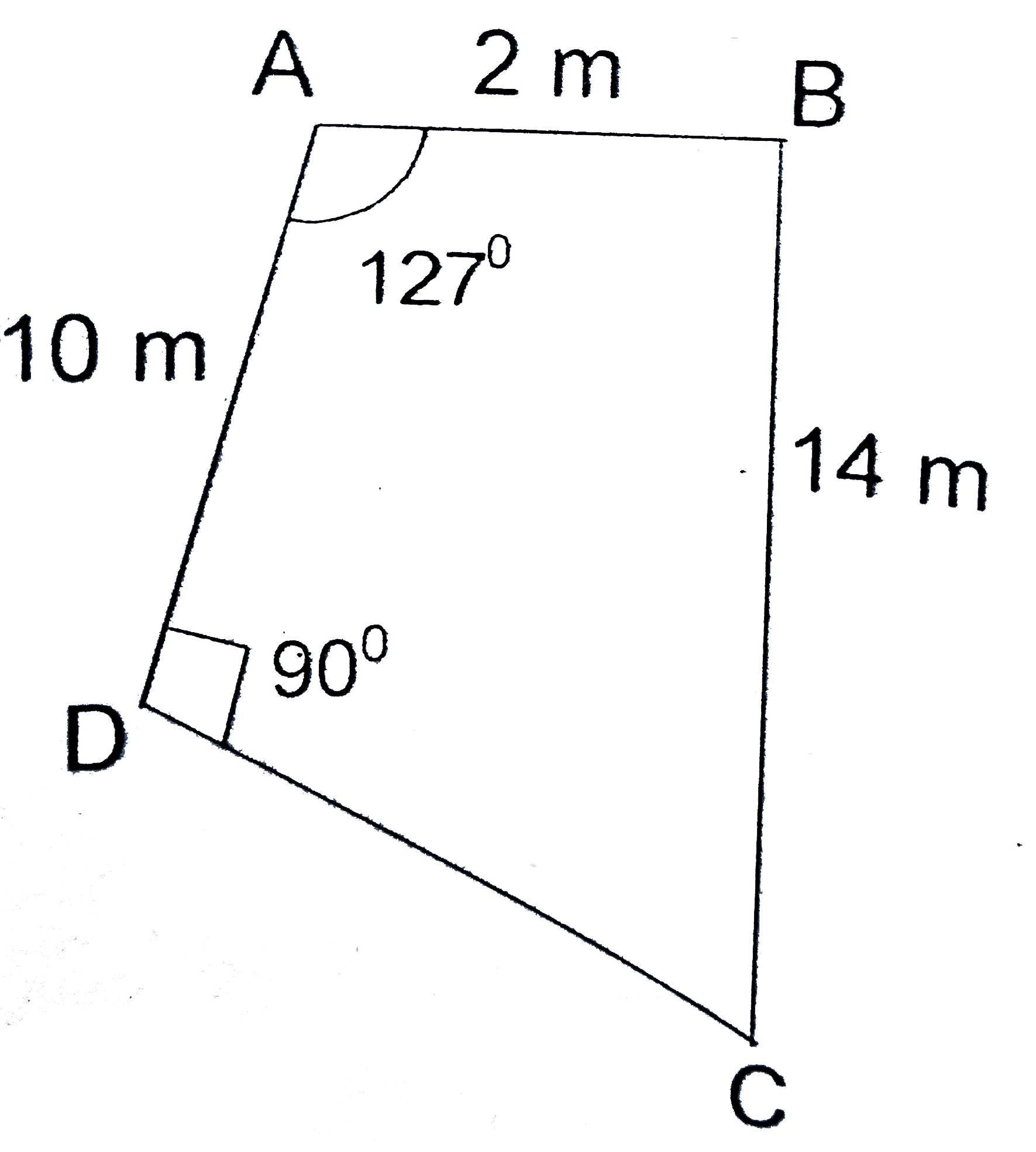
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is

View Solution
