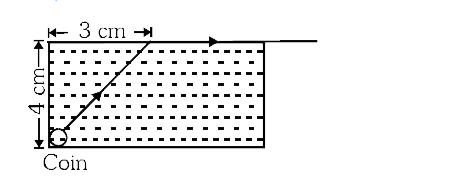
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
2.4×108m/s
3.0×108m/s
1.2×108m/s
1.8×108m/s
The correct Answer is:D
From figure, sinC=⎛⎜
⎜⎝3√(4)2+(3)2=35
where C is the critical angle. Also, sinC=lμg
sinC=1aμl[sincelμa=1aμl]
Also, aμl=velocity of light in air (c)velocity of light in liquid (v)
∴sinC=vc=v3×108
or v=3×108×35=1.8×108ms−1
Topper's Solved these Questions
Similar Questions
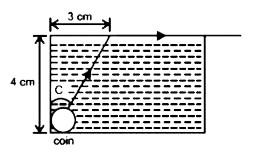
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)
How fast is the light travelling in the liquid ?
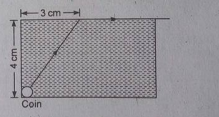
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

View Solution
Knowledge Check
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid?
 A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1
A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?

A1.8×108ms−1B2.4×108ms−1C3.0×108ms−1D1.2×108ms−1A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light travelling in the liquid ?A1.8×108m/sB2.4×108m/sC3.0×108m/sD1.2×108m/s
A ray of light travelling in air falls obliquely on the surface of a clam poun. It will
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
View SolutionA beaker of radius 15 cm is filled with a liquid of surface tension 0.075 N/m. Force across an imaginary diameter on the surface of the liquid is
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View Solution
