In the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .
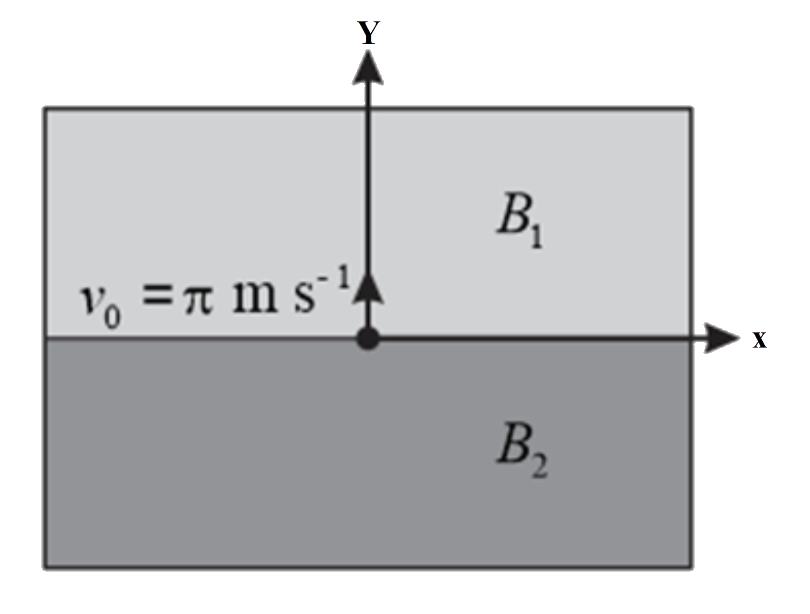
The correct Answer is:1.2
(i) Average speed along x - axis
(vx)=∫|→x|dt∫dt=d1+d2t1+t2
(ii) We have,
r1=mvqB1,r2=mvqB2
Since, B1=B24
∴r1=4r2
Time in B1→xmqB1=t1
Time in B2⇒πmqB2=t2
Total distance along x - axis.
d1+d2=2r1−2r2=2(r1−r2)=2(3r2)=6r2
Total time T=t1+t2=5t2
∴ Average speed =6r25t2=6mv5qB2×qB2πm=65=1.2
Topper's Solved these Questions
Similar Questions
A region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity −−→V=V0ˆi+V0ˆj . After some time the velocity of the particle was observed to beV0ˆJ while its x co-ordinate was positive. Write all possible values of EB
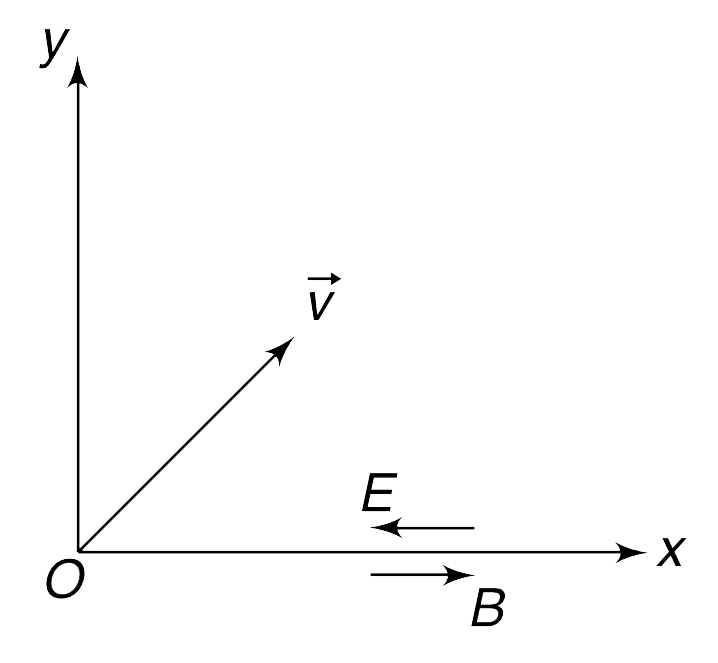
View SolutionA uniform magnetic field exists perpendicular to the plane of the figure and a uniform electric field exists in the plane of the figure in positive y direction. A charged particle, when projected along xy plane moves along the path shown in the figure. Is the particle positively charged or negatively charged?
View Solution
Knowledge Check
A uniform electric field →E in the y-direction and uniform magnetic field →B in the x-direction exists in free space. A particle of mass m and carrying charge g is projected from the origin with speed v0 along the y axis. The speed of the particle as a function of its y coordinate will be
A√v20+2qEymB√v20+qEymC√v20+4qEymDv0A uniform magnetic field of magnitude 1T exists in region y≥0 along ˆk direction as shown. A particle of charge 1C is projected from point (−√3,−1) towards origin with speeds 1m/sec. If mass of particle moves are:
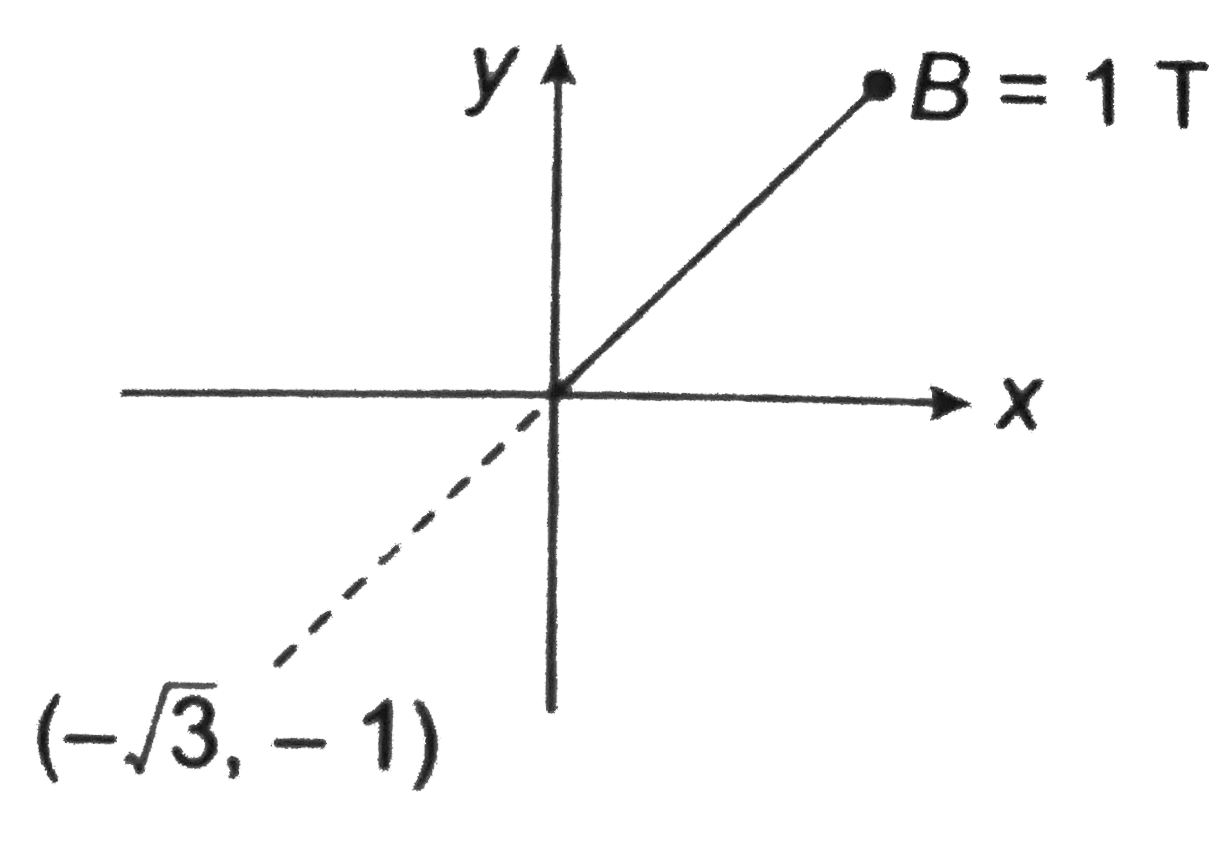 A(1,√3)B(1,−√3)C(12,−√32)D(√32,−12)
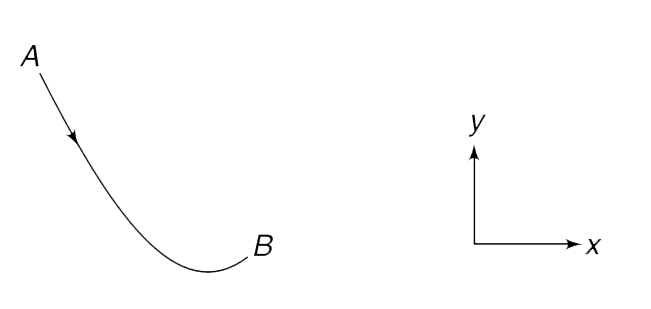
A(1,√3)B(1,−√3)C(12,−√32)D(√32,−12)A positively charged particle is moving with a speed v in the region of uniform magnetic induction field B as shown in figure. Which of the following statements is correct?
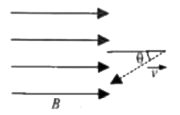 AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the reader
AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the reader
A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
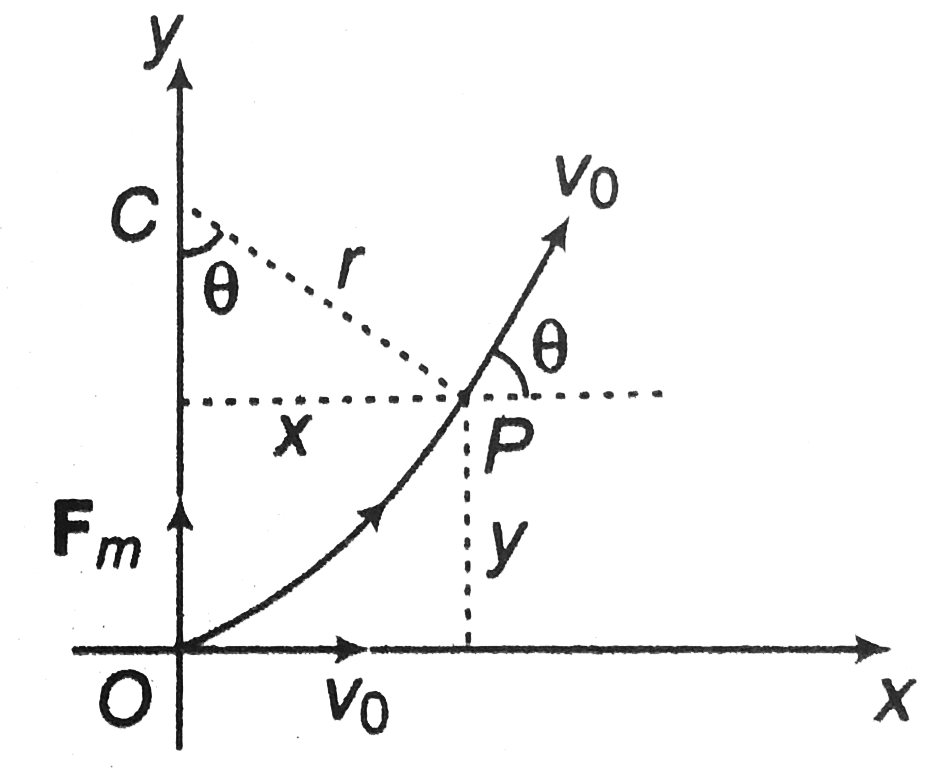
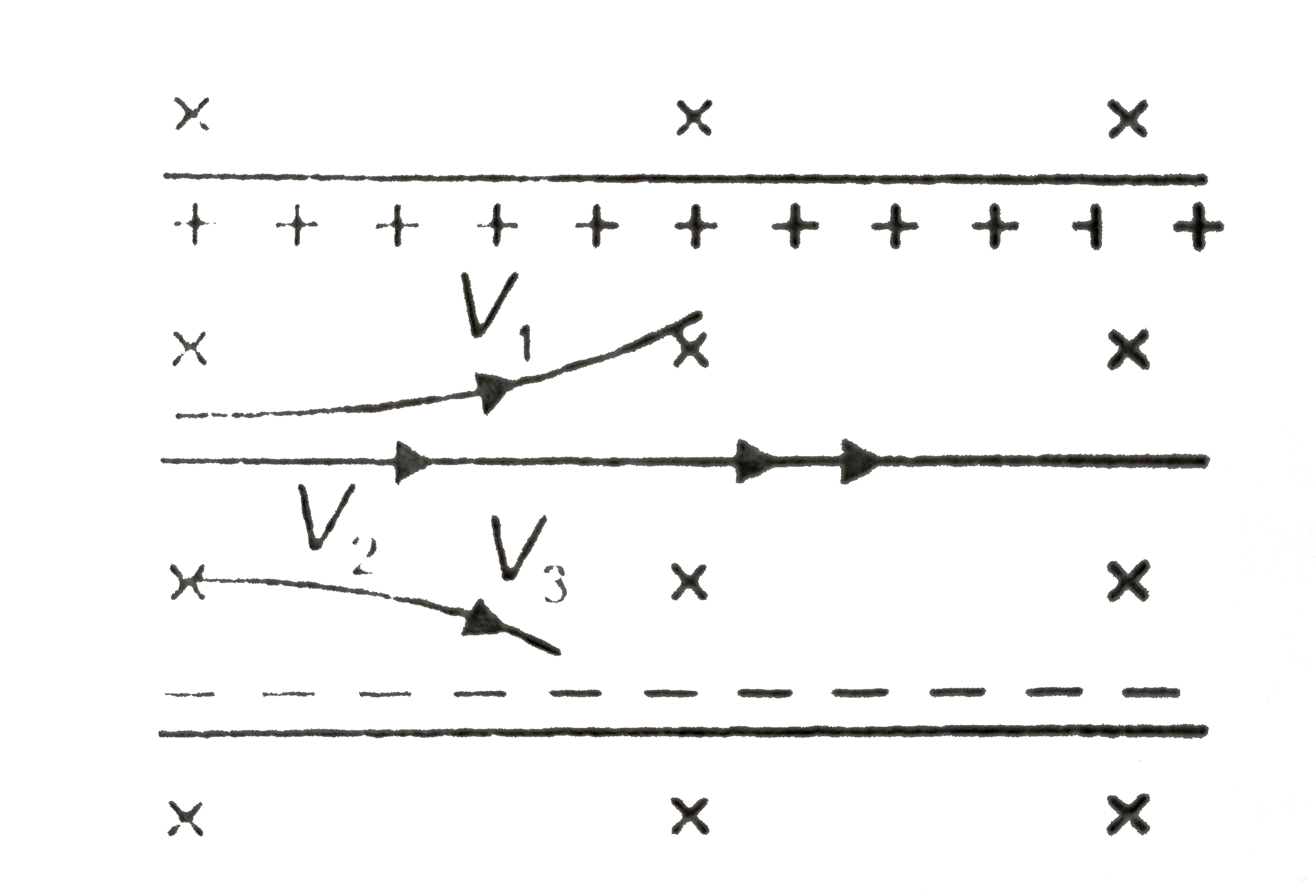
View SolutionIn a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
View SolutionThere is a uniform electric field of strength 103V/m along y-axis. A body of mass 1g and charge 10−6C is projected into the field from origin along the positive x-axis with a velocity 10m/s. Its speed in m/s after 10s is (Neglect gravitation)
View SolutionA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
View SolutionA uniform magnetic field B=B0ˆj exists in space. A particle of mass m and charge q is projected towards X-axis with speed v from a point (a,0, 0). The maximum value of v for which the particle does not hit the Y-Z plane is
View Solution
