If the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-

A

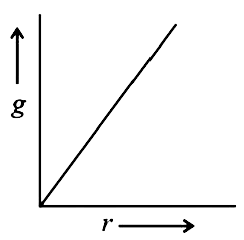
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Here r is the radius of the planet. Then, the acceleration due to gravity at the surface of the planet,
$g = \frac{G M}{r^{2}} = \frac{G_{ρ} \frac{4}{3} π r^{3}}{r^{2}} = \frac{4}{3} π G ρ r$
This meang increases linearly with increase in r, keeping density constant. Hence, the graph is straight line.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-
A
B
C
D
Question 2 - Select One
If the radius of a planet is R and its density is $ρ$ , the escape velocity from its surface will be
A $v_{e} \propto ρ R$
B $v_{e} \propto \sqrt{ρ} R$
C $v_{e} \propto \frac{\sqrt{ρ}}{R}$
D $v_{e} \propto \frac{1}{\sqrt{ρ} R}$
Question 3 - Select One
If different planets have the same density but diferent radii then the acceleration due to gravity (g) on the surface of the planet will depend on its radius (R) as
A $g \propto \frac{1}{R^{2}}$
B $g \propto \frac{1}{R}$
C $g \propto R$
D $g \propto R^{2}$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 108-PHYSICS (SUBJECTIVE NUMERICAL)

Home
Ask Doubt
Profile