In the arrangement shown in the diagram, pulleys are small and springs are ideal. $k_{1} = k_{2} = k_{3} = k_{4} = 10 N m^{- 1}$ are force constants of the springs and mass $m = 10 k g .$ If the time period of small vertical oscillations of the block of mass m is given by $2 π x$ seconds, then find the value of x.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $4$

$T = 2 π s q t (\frac{m}{K_{e q}})$
where $K_{e q} = \frac{1}{4 [\frac{1}{k_{1}} + \frac{1}{k_{2}} + \frac{1}{k_{3}} + \frac{1}{k_{4}}]} = \frac{10}{16}$
$T = 2 π \sqrt{\frac{m}{K_{e q}}} = 2 π x$
So $x = \sqrt{\frac{10}{10 / 16}} = 4, x = 4$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
A $2 π \sqrt{\frac{m}{k}}$
B $π \sqrt{\frac{m}{k}}$
C $4 π \sqrt{\frac{m}{k}}$
D $2 π \sqrt{\frac{m}{2 k}}$
Question 2 - Select One
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)

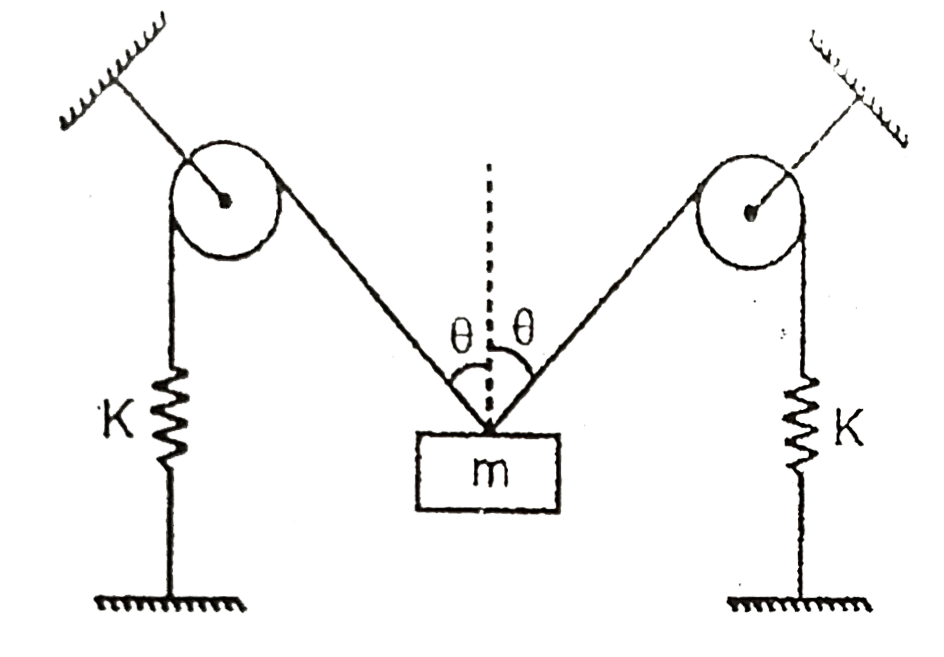A $2 π cos θ \sqrt{\frac{m}{2 k}}$
B $2 π sec θ \sqrt{\frac{m}{2 k}}$
C $2 π sin θ \sqrt{\frac{m}{2 k}}$
D $2 π cos e c θ \sqrt{\frac{m}{2 k}}$
Question 3 - Select One
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

A $2 π \sqrt{\frac{m}{k}}$
B $2 π \sqrt{\frac{m}{2 k}}$
C $2 π \sqrt{\frac{m}{3 k}}$
D $π \sqrt{\frac{m}{k}}$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 113-PHYSICS

Home
Ask Doubt
Profile