The objective function is maximum or minimum at a point, which lies on the boundary of the feasible region .Solution in Punjabi
Step by step video & image solution for The objective function is maximum or minimum at a point, which lies on the boundary of the feasible region . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE156videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - INVERSE-TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE111videos
INVERSE-TRIGONOMETRIC FUNCTIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - EXERCISE232videos
MATRICES
Similar Questions
Draw the graph of the following LPP: 3x+y≤17,x≥0,y≥0.
01:11View SolutionFind the value of cos−1(cos(3π2))
03:14View SolutionIf a matrix has 8 elements, what are the possibles orders it can have?
00:29View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
01:21View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
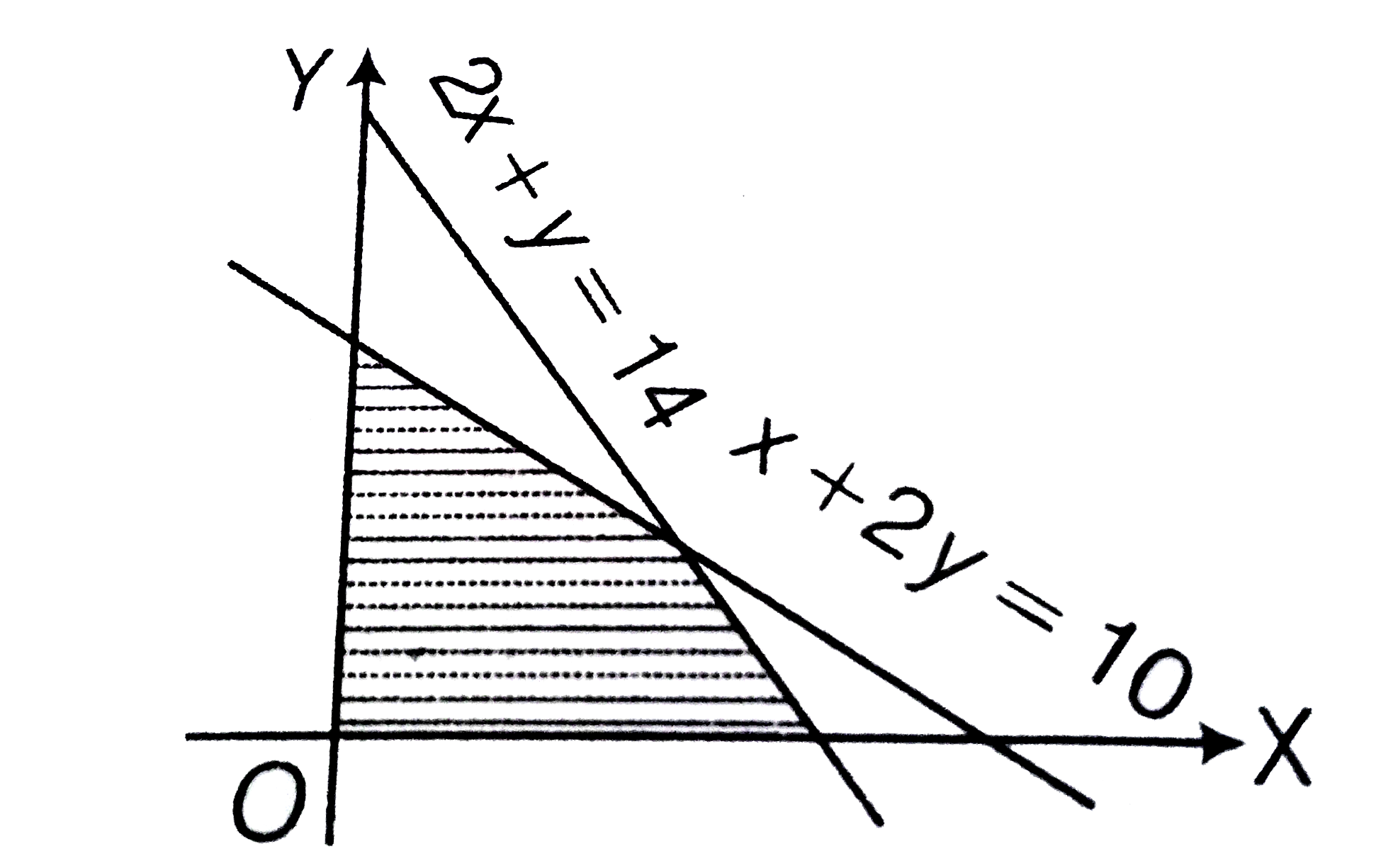 View Solution
View SolutionWhich of the following statements is false? A) The feasible region is always a concave region B) The maximum (or minimum) solution of the objective function occurs at the vertex of the feasible region C) If two corner points produce the same maximum (or minimum) value of the objective function, then every point on the line segment joining these points will also give the same maximum (or minimum) two. values D) All of the above
04:24View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?01:24View SolutionThe maximum or minimum of the objective funtion occurs only at the corner points of the feasible region. This theorem is known as fundamental theorem of
01:46View SolutionThe, objective function is maximum or minimum at a point, which lies on the boundary of the feasible region.
02:17View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
02:20View SolutionA corner point of a feasible region is a point in the region which is the ……….. of two boundary lines.
01:53View SolutionIf the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionIn a LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
02:05View Solutionसुसंगत क्षेत्र के सभी बिंदुओं के अधिकतम या न्यूनतम उद्देश्य फलन के लिए बिंदु है। (a) सुसंगित क्षेत्र के अंदर (b) सुसंगित क्षेत्र की परिसीमा पर (c) सुसंगित क्षेत्र की परिसीमा के शीर्ष पर (d) कोई नहीं
02:20View SolutionOf all the points of feasible region, the optimal value is obtained at the boundary of the feasible region.
01:01View SolutionIf the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
01:20View Solution

