Which of the following statements is false? A) The feasible region is always a concave region B) The maximum (or minimum) solution of the objective function occurs at the vertex of the feasible region C) If two corner points produce the same maximum (or minimum) value of the objective function, then every point on the line segment joining these points will also give the same maximum (or minimum) two. values D) All of the above
The feasible region is always a concave region
The maximum (or minimum) solution of the objective function occurs at the vertex of the feasible region
If two corner points produce the same maximum (or minimum) value of the objective function, then every point on the line segment joining these points will also give the same maximum (or minimum) two. values
All of the above
The correct Answer is:A
The feasible region is always a convex region.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )15videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )30videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner3videos
LINE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER22videos
MATHEMATICAL LOGIC
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum or minimum of the objective funtion occurs only at the corner points of the feasible region. This theorem is known as fundamental theorem of
AAlgebraBArithmeticCCalculusDExtreme point
Maximum and minimum value of function in its domain
View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View SolutionIf the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
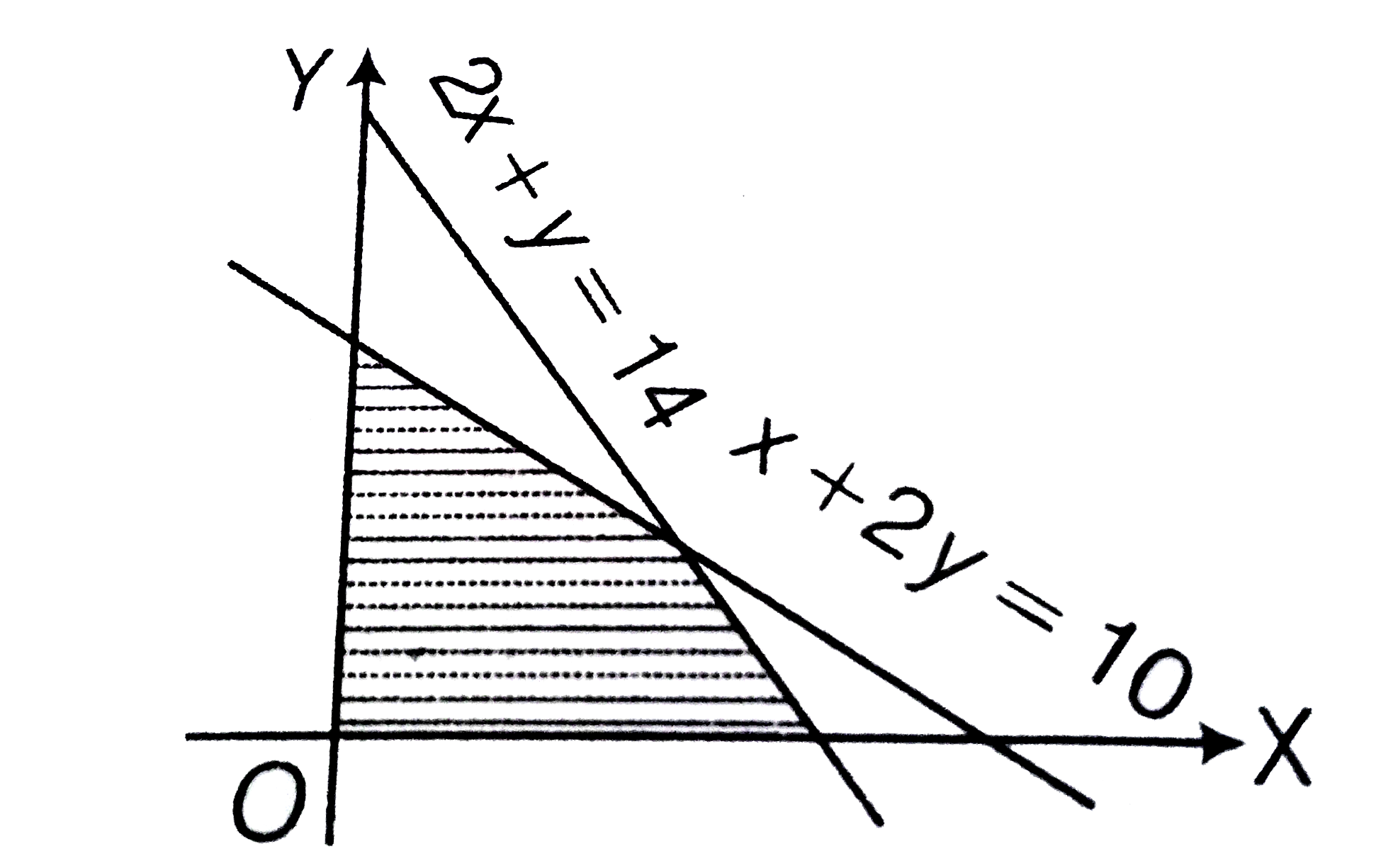 View Solution
View SolutionWhich of the following functions has maximum or minimum value ?
View SolutionMaximum and Minimum Value of Rational Function
View SolutionThe maximum value of objective function Z=3x+y under given feasible region is
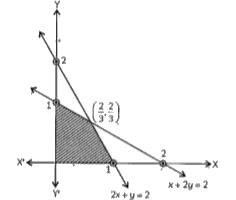 View Solution
View Solution

