Given that PQ = 16 m, KB = 16 m,
PH = 35 m and QK = 20 m, Find:
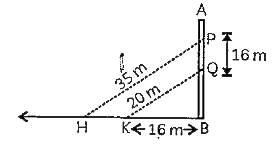
Find BQ.
The correct Answer is:12 m
Step by step video, text & image solution for Given that PQ = 16 m, KB = 16 m, PH = 35 m and QK = 20 m, Find: Find BQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-II) TYPE QUESTIONS21videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS10videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS10videos
TRIANGLES
- BOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS30videos
SURFACE AREAS AND VOLUMES
Similar Questions
Given that PQ = 16 m, KB = 16 m,
PH = 35 m and QK = 20 m, Find HK
 View Solution
View SolutionTwo spotlights, P and Q are mounted on a vertical pole AB as shown.
Light beams from P and Q shine to two points on the ground, H and K, respectively. Given that PQ = 16m, KB = 16m, PH = 35m and QK = 20m, Find:
HK, the distance between the projections of the light beams.View Solution
Knowledge Check
- Question 1 - Select One
In a rectangle ABCD , E is the mid -point of AB . If AB= 16 m and AD = 6 m , then find ED .
A15 cmB10 cmC12 mD14 m - Question 2 - Select One
Find the G.M. of 4 and 16.
A8B10C9D12
If m−n=16andm2+n2=400, then find mn.
View SolutionFind the area of the given trapezium PQRS in which RQ || SP and PQ ⊥ SP such that RQ = 7m, RS = 13 m and SP = 12 m.
View SolutionFind the value of m:
4m + 16 =0View SolutionLet AP and BQ be two vertical poles at points A and B, respectively. If AP=16m,BQ=22mandAB=20m, then find the distance of a point R on AB from the point A such that RP2+RQ2is minimum.
View SolutionABCD is a parallelogram, AE⊥DCand CF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
View SolutionLet AP and BQ be two vertical poles at points A and B respectively. If AP=16m, BQ=22m and AB=20m , then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View Solution

