Question

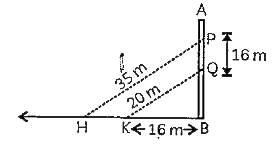
Two spotlights, P and Q are mounted on a vertical pole AB as shown.
Light beams from P and Q shine to two points on the ground, H and K, respectively. Given that PQ = 16m, KB = 16m, PH = 35m and QK = 20m, Find:
HK, the distance between the projections of the light beams.

Answer

5m

Explanation

To solve the problem, we need to find the distance HK, which is the distance between the projections of the light beams from points P and Q to the ground at points H and K respectively.

1. Identify the Given Values:
- PQ = 16 m (distance between the two spotlights)
- KB = 16 m (distance from point K to point B, the base of the pole)
- PH = 35 m (distance from point P to point H)
- QK = 20 m (distance from point Q to point K)

2. Find BQ using Triangle QBK:
- Since triangle QBK is a right triangle, we can apply the Pythagorean theorem:
\( BQ^2 = QK^2 - KB^2 \)
- Substitute the values:
\( BQ^2 = 20^2 - 16^2 \)
\( BQ^2 = 400 - 256 = 144 \)
- Therefore, taking the square root:
\( BQ = \sqrt{144} = 12 \text{ m} \)

3. Find HB using Triangle PBH:
- Now, we will use triangle PBH to find HB. Again, we apply the Pythagorean theorem:
\( PH^2 = PB^2 + HB^2 \)
- We know PH = 35 m and PB = BQ = 12 m (since PB is the same as BQ):
\( 35^2 = 12^2 + HB^2 \)
\( 1225 = 144 + HB^2 \)
- Rearranging gives:
\( HB^2 = 1225 - 144 = 1081 \)
- Taking the square root:
\( HB = \sqrt{1081} \approx 32.9 \text{ m} \)

4. Calculate HK:
- Finally, we can find HK:
\( HK = HB - KB \)
- Substitute the values:
\( HK = 32.9 - 16 = 16.9 \text{ m} \)

Final Answer:
The distance HK is approximately 16.9 m.