In ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
3.6cm
2.8cm
2.4cm
1.8cm
To solve the problem, we will use the Basic Proportionality Theorem (also known as Thales's theorem), which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Values:
- AE = 1.8 cm
- BD = 7.2 cm
- CE = 5.4 cm
- Let AD = x (the length we need to find).
2. Apply the Basic Proportionality Theorem:
According to the theorem, we have:
ADBD=AEEC
Substituting the known values:
x7.2=1.85.4
3. Simplify the Right Side:
To simplify 1.85.4:
- Divide both the numerator and the denominator by 1.8:
1.8÷1.85.4÷1.8=13
Thus, we have:
x7.2=13
4. Cross-Multiply:
Cross-multiplying gives:
3x=7.2
5. Solve for x:
Now, divide both sides by 3:
x=7.23=2.4 cm
6. Conclusion:
Therefore, the length of AD is:
AD=2.4 cm
- AE = 1.8 cm
- BD = 7.2 cm
- CE = 5.4 cm
- Let AD = x (the length we need to find).
According to the theorem, we have:
ADBD=AEEC
Substituting the known values:
x7.2=1.85.4
To simplify 1.85.4:
- Divide both the numerator and the denominator by 1.8:
1.8÷1.85.4÷1.8=13
Thus, we have:
x7.2=13
Cross-multiplying gives:
3x=7.2
Now, divide both sides by 3:
x=7.23=2.4 cm
Therefore, the length of AD is:
AD=2.4 cm
Topper's Solved these Questions
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section -B
20 Videos
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 10 SOLVED BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 SOLVED EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
Knowledge Check
In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cmABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
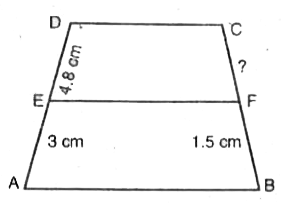 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseIn ΔABC, D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then ar(ΔADE)ar(ΔABC) is
A49B1681C425D25
In △ABC, D and E are points on the sides AB and AC, respectively, such that DE || BC. If AD = 5cm, DB = 9cm AE =4cm and BC = 15.4cm, then the sum of the length of DE and EC (in cm) is:
△ABC में, D और E क्रमशः AB और AC भुजाओं पर बिंदु इस प्रकार है की DE||BC, यदि AD = 5cm, DB = 9cm AE = 4cm और BC = 15.4cm है, तो DE और EC (सेमी में) की लंबाई का योग है
View SolutionIn △ABC ,D and E are the points on sides AC and AB, respectively, such that ∠ADE=∠B. If AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then DE is equal to:
त्रिभुज ABC में, D तथा E भुजा AC और AB पर स्थित ऐसे बिंदु ∠ADE=∠B है| यदि AD =7.6 सेमी, AE = 7.2 सेमी, BE = 4.2 सेमी तथा BC = 8.4 सेमी है, तो DE किसके बराबर है ?
View SolutionP and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionIf D and E are points on the sides AB and AC respectively of DetlaABC such that AB=5.6cm,AD=1.4cm,AC=7.2cmandAE=1.8cm. Show that DE∣∣BC.
View SolutionIn ΔABC,D and E are points on the sides AB and AC respectively. Find whether DE||BC if
(i) AD= 3cm , BD = 4.5cm, AE = 4cm, AC= 10cm
(ii) AB=7 cm , BD = 4.5cm, AE = 3.5 cm, CE= 5.6cm.
View Solution