The feasible region of a system of linear inequalities is shown shaded in the following graph . If the objective function is Z = ax + by where a,b are constants and the maximum of Z occurs at points A and D then :
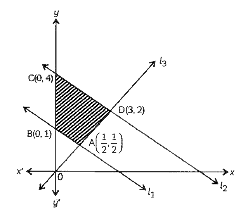
3a=5b
a=−35b
4a=7b
a = −47 b
The correct Answer is:B
Step by step video & image solution for The feasible region of a system of linear inequalities is shown shaded in the following graph . If the objective function is Z = ax + by where a,b are constants and the maximum of Z occurs at points A and D then : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The feasible region by a system of linear inequalities is shown shaded in the given graph.
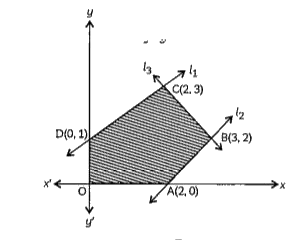
If Z = 4x - 6y, then Zmin =
View SolutionThe feasible region of a system of linear inequalities is shown below. If the objective function is maximise Z = 25x + 15y, then the maximum value of Z occurs at:
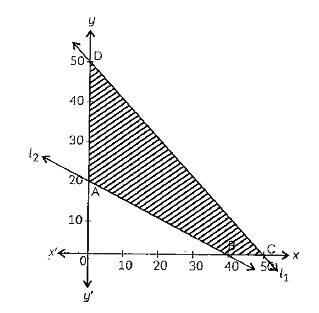
View Solution
Knowledge Check
The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
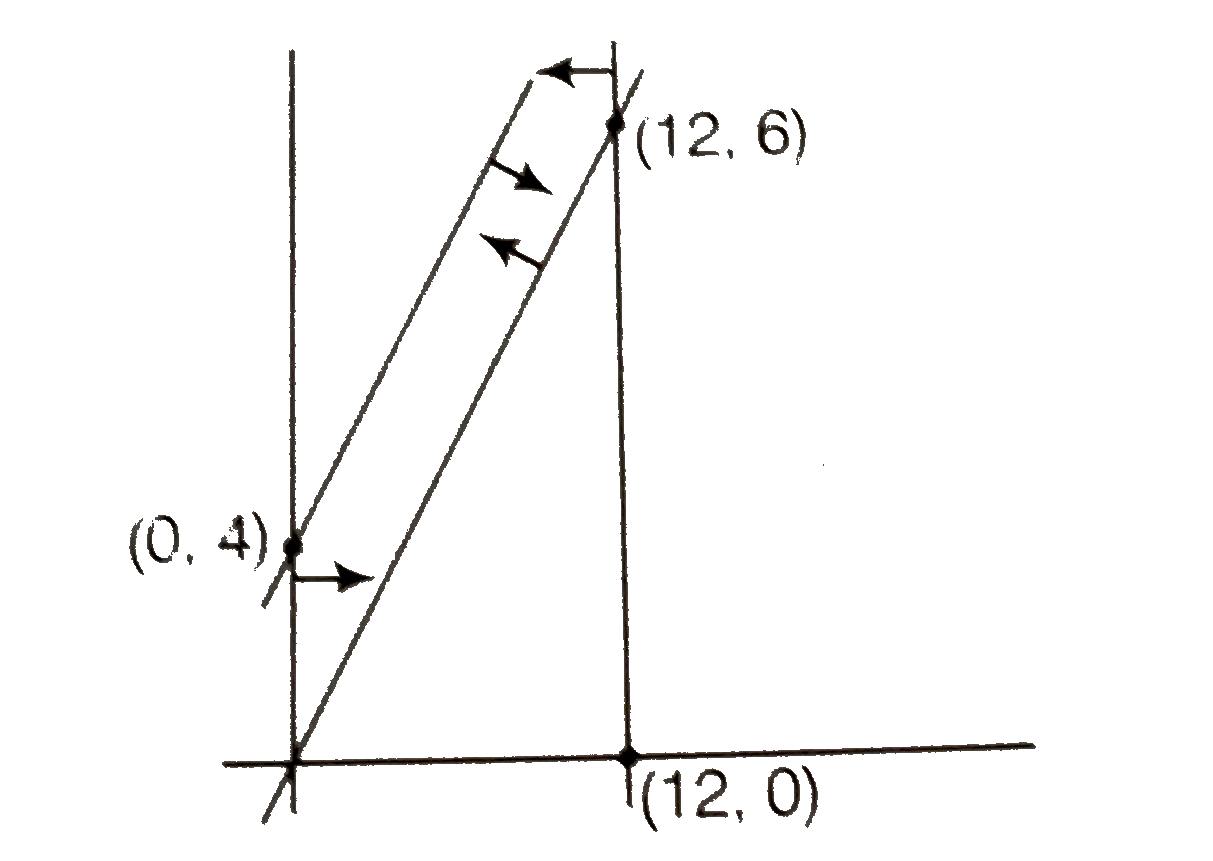 A0B8C12D−18
A0B8C12D−18In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
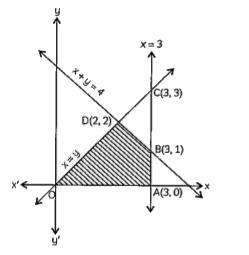 AOBBCCDD
AOBBCCDDIf the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101
The feasible region of a system of linear inequations is shown shaded in the following figure If Z=4x+3y, then Zmax−Zmin=
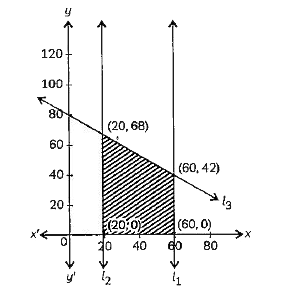
View SolutionThe feasible region of a sytem of linear inequations is shown below. If Z = 2x + y, then the minimum value of Z is:
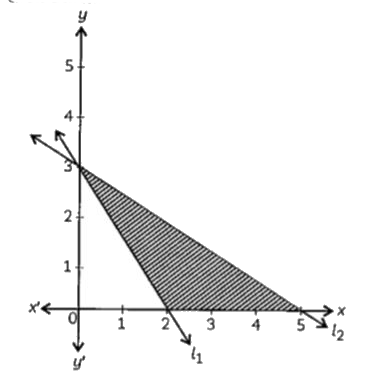
View SolutionThe corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
View Solution
