R is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
n2R
nR
Rn
Rn2
The correct Answer is:D
To find the equivalent resistance of n resistors of the same resistance R when connected in parallel, we can follow these steps:
Step 1: Understand the Series Connection
When n resistors of resistance r are connected in series, the equivalent resistance R is given by:
R=n⋅r
This means that if you have n resistors, the total resistance is simply the sum of all individual resistances.
Step 2: Find the Resistance of a Single Resistor
From the equation above, we can express the resistance of a single resistor r in terms of the equivalent resistance R:
r=Rn
Step 3: Understand the Parallel Connection
When these n resistors are connected in parallel, the formula for equivalent resistance Req is given by:
1Req=1r+1r+…+1r(n times)
This simplifies to:
1Req=n⋅1r
Step 4: Substitute the Value of r
Now, substituting r from Step 2 into the equation:
1Req=n⋅1Rn=n⋅nR=n2R
Step 5: Solve for Req
Taking the reciprocal to find Req:
Req=Rn2
Conclusion
Thus, the equivalent resistance Req of n resistors of the same resistance R when connected in parallel is:
Req=Rn2
When n resistors of resistance r are connected in series, the equivalent resistance R is given by:
R=n⋅r
This means that if you have n resistors, the total resistance is simply the sum of all individual resistances.
From the equation above, we can express the resistance of a single resistor r in terms of the equivalent resistance R:
r=Rn
When these n resistors are connected in parallel, the formula for equivalent resistance Req is given by:
1Req=1r+1r+…+1r(n times)
This simplifies to:
1Req=n⋅1r
Now, substituting r from Step 2 into the equation:
1Req=n⋅1Rn=n⋅nR=n2R
Taking the reciprocal to find Req:
Req=Rn2
Thus, the equivalent resistance Req of n resistors of the same resistance R when connected in parallel is:
Req=Rn2
Topper's Solved these Questions
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -B
24 Videos
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C
6 Videos
- SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C
6 Videos
Similar Questions
Knowledge Check
The equivalent resistance of resistors connected in series is always
AEqual to the mean of component resistorsBLess than the lowest of component resistorsCIn between the lowest and the highest of component resistorsDEqual to sum of component resistorsThe equivalent resistance in series combination is
Asmaller than the largest resistanceBlarger than the largest resistanceCsmaller than the smallest resistanceDlarger than the smallest resistanceThe equivalent resistance of n identical resistors connected in parallel is x. If the resistors are connected in series, the equivalent resistance would be
An xBn2xCx/nDx/n2
Two resistance R1andR2 when connected in series produce equivalent resistance equal to x. and when the same two resistance are connected in parallel then equivalent resistance becomes y. Calculate the product of magnitudes of R1andR2 in terms of x and y.
View SolutionIf two equal resistances are connected in parallel the equivalent resistance is halved.
View SolutionFind an expression for the equivalent resistance of three resistors joined in series.
View SolutionFind the equivalent resistance between A and B. Each resistor has same resistance R.
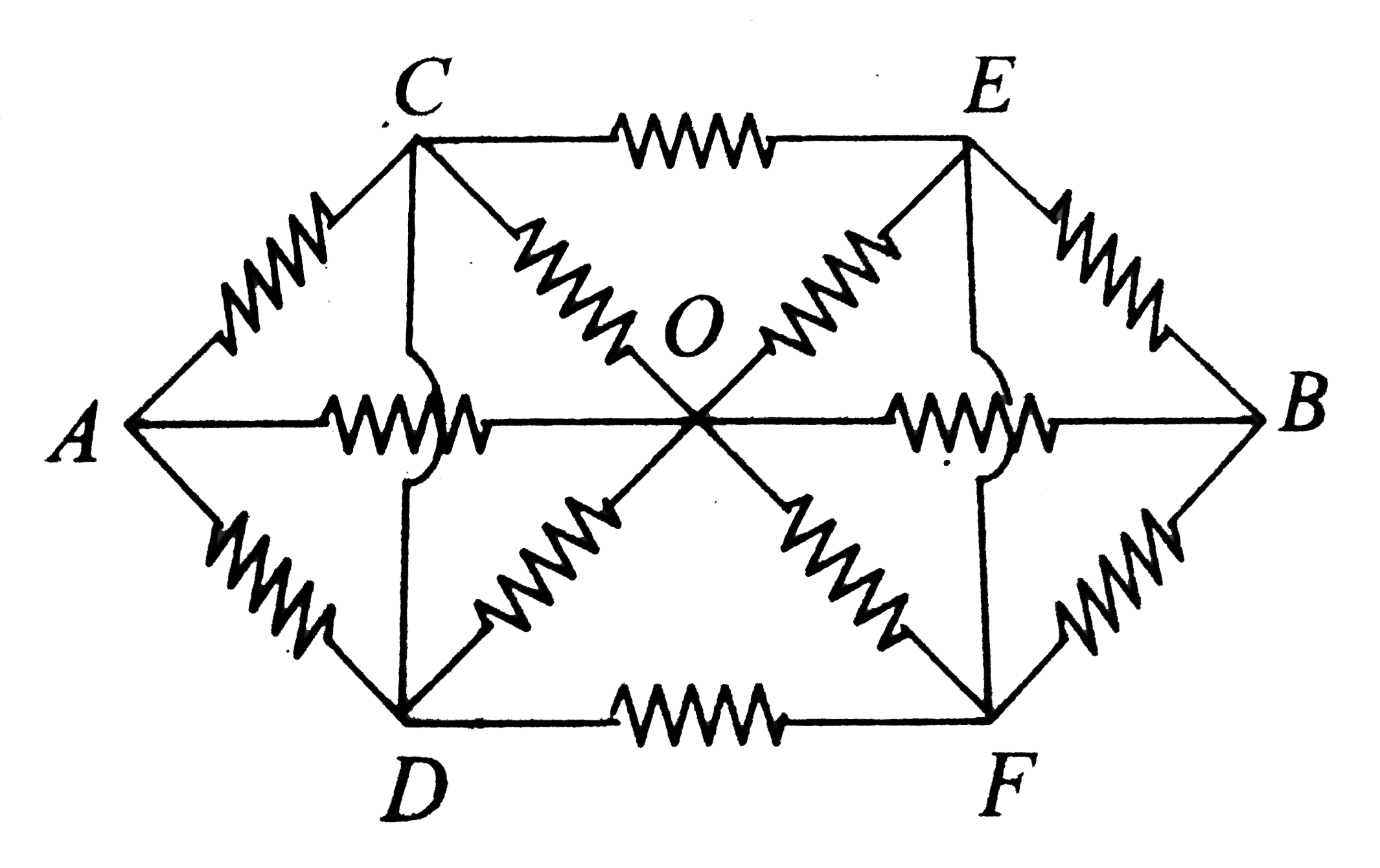
View SolutionThe equivalent resistance of n identical resistors connected in parallel si x. If the resistors are connected in series, the equivalent resistance would be.
View Solution
