The equivalent resistance of number of resistors will be lesser,if they are connected in..
To solve the question regarding the equivalent resistance of resistors connected in different configurations, we need to understand the concepts of series and parallel connections.
1. Understanding Resistor Connections:
- Resistors can be connected in two main configurations: series and parallel.
- In a series connection, the total or equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2+R3+…
- In a parallel connection, the total or equivalent resistance is given by the formula:
1Req=1R1+1R2+1R3+…
2. Comparing the Two Configurations:
- When resistors are connected in series, the equivalent resistance increases because you are adding up all the resistances.
- In contrast, when resistors are connected in parallel, the equivalent resistance decreases because you are effectively providing multiple paths for current to flow.
3. Analyzing the Parallel Connection:
- For two resistors R1 and R2 connected in parallel, the formula can be rewritten as:
Req=R1⋅R2R1+R2
- This formula indicates that the equivalent resistance (R_eq) will always be less than the smallest individual resistor (either R1 or R2).
4. Conclusion:
- Therefore, the equivalent resistance of a number of resistors will be lesser if they are connected in parallel.
Final Answer:
The equivalent resistance of a number of resistors will be lesser if they are connected in parallel.
---
- Resistors can be connected in two main configurations: series and parallel.
- In a series connection, the total or equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2+R3+…
- In a parallel connection, the total or equivalent resistance is given by the formula:
1Req=1R1+1R2+1R3+…
- When resistors are connected in series, the equivalent resistance increases because you are adding up all the resistances.
- In contrast, when resistors are connected in parallel, the equivalent resistance decreases because you are effectively providing multiple paths for current to flow.
- For two resistors R1 and R2 connected in parallel, the formula can be rewritten as:
Req=R1⋅R2R1+R2
- This formula indicates that the equivalent resistance (R_eq) will always be less than the smallest individual resistor (either R1 or R2).
- Therefore, the equivalent resistance of a number of resistors will be lesser if they are connected in parallel.
The equivalent resistance of a number of resistors will be lesser if they are connected in parallel.
Topper's Solved these Questions
Similar Questions
A student did the experiment to find the equivalent resistance of two given resistors, R1 and R2 first when they are connected in series and next when they are connected in parallel. The two values of the equivalent resistance obtained by him were Rs and Rp respectively. Compare Rs and Rp.
View SolutionA student did the experiment to find the equivalent resistance of two given resistors, R1 and R2 first when they are connected in series and next when they are connected in parallel. The two values of the equivalent resistance obtained by him were Rs and Rp respectively. Compare Rs and Rp.
View Solution
Knowledge Check
R is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
An2RBnRCRnDRn2In the experiment on finding the equivalent resistance of two resistors connected in series, three students connected the ammeter in their circuits in the three ways X, Y and Z shown here.
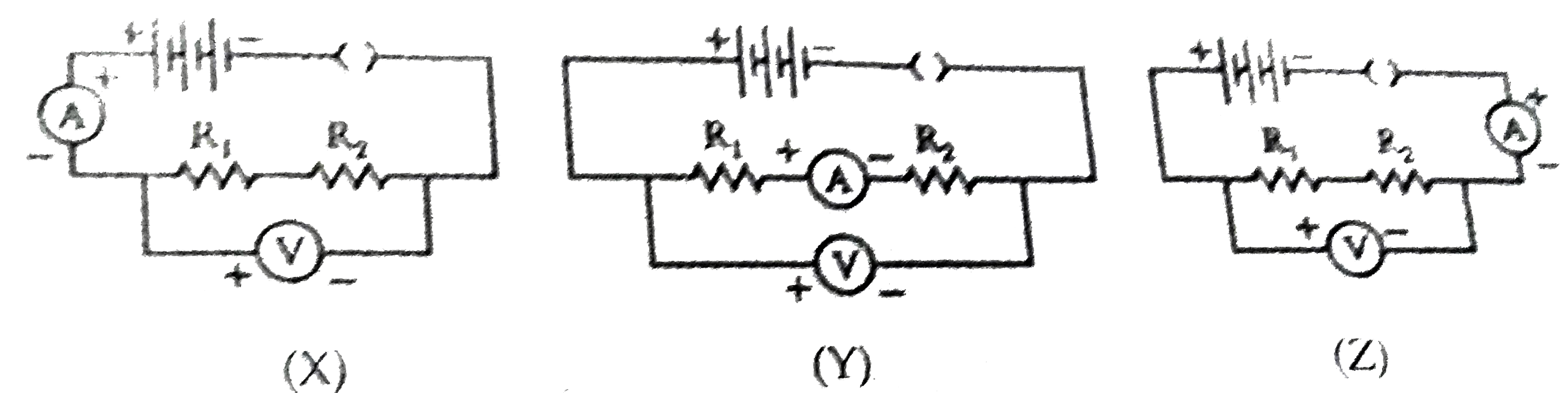
Assuming their ammeters to be ideal, the ammeters have been correctly connected inAcases X and Y onlyBcases Y and Z onlyCcases Z and X onlyDall the three casesIn the experiment on finding the equivalent resistance of two resistors, connected in parallel, three students connected the voltmeter in their circuits, in the three ways X, Y and Z shown here.
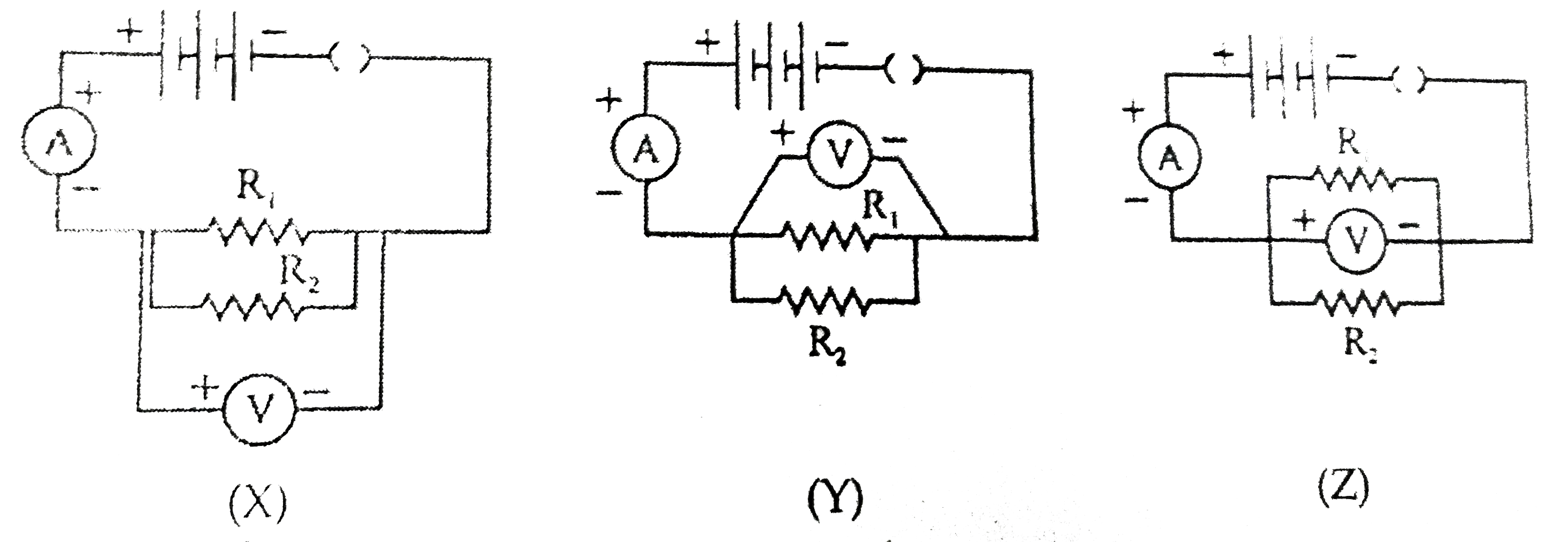
The voltmeter has been correctly connected inAcases X and Y onlyBcases Y and Z onlyCcases Z and X onlyDall the three cases
The equivalent resistance of resistors connected in series is always
View SolutionThe equivalent resistance of network of three 4Ω resistors can not be
View SolutionThe equivalent resistance of network of three 2Ω resistors can not be
View SolutionThe equivalent resistance of network of three 4Ω resistors can not be
View SolutionFour student have made the following circuit diagrams for determining the equivalent resistance of two resistors connected in series :
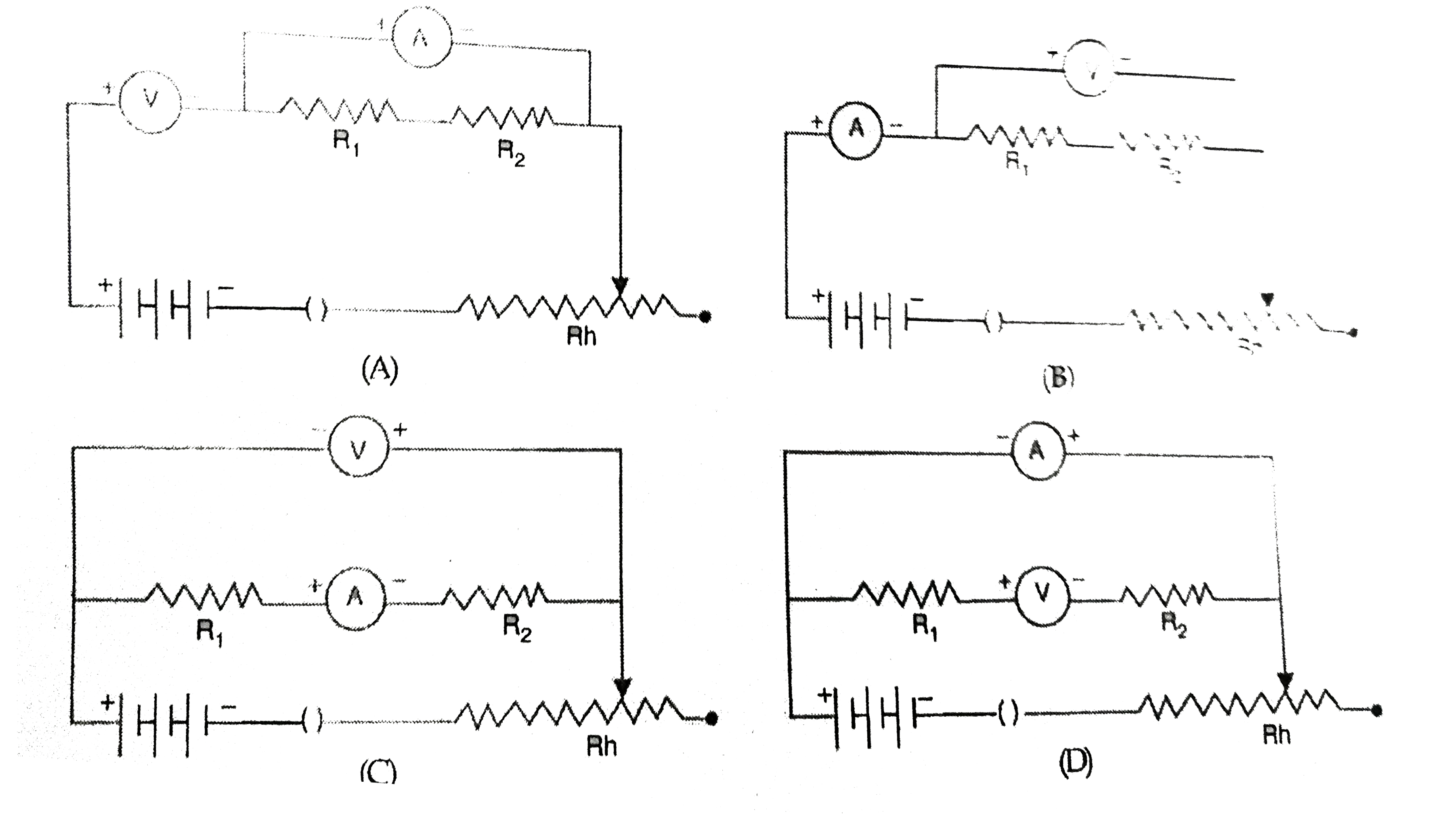
The correct circuit diagram is :
View Solution
