A particle of mass m, charge e and velocity v moving in a magnetic field B perpendicular to the motion of particle. The radius of its path is:
Bemv
evBm
Bvem
mvBe
The correct Answer is:D
To find the radius of the path of a charged particle moving in a magnetic field, we can follow these steps:
1. Identify the Given Parameters:
- Mass of the particle, m
- Charge of the particle, e
- Velocity of the particle, v
- Magnetic field strength, B
2. Understand the Motion:
- The particle is moving in a magnetic field that is perpendicular to its velocity. This means that the magnetic force will act as a centripetal force, causing the particle to move in a circular path.
3. Apply the Formula for Radius:
- The radius R of the circular path of a charged particle in a magnetic field is given by the formula:
R=mveB
- Here, mv is the momentum of the particle, and eB is the magnetic force acting on the particle.
4. Substitute the Values:
- In this case, we directly substitute the known quantities into the formula:
R=mveB
5. Final Expression:
- The final expression for the radius of the path of the particle is:
R=mveB
- Mass of the particle, m
- Charge of the particle, e
- Velocity of the particle, v
- Magnetic field strength, B
- The particle is moving in a magnetic field that is perpendicular to its velocity. This means that the magnetic force will act as a centripetal force, causing the particle to move in a circular path.
- The radius R of the circular path of a charged particle in a magnetic field is given by the formula:
R=mveB
- Here, mv is the momentum of the particle, and eB is the magnetic force acting on the particle.
- In this case, we directly substitute the known quantities into the formula:
R=mveB
- The final expression for the radius of the path of the particle is:
R=mveB
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C6videos
SAMPLE PAPER 3
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C6videos
SAMPLE PAPER 3
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2EXERCISE - SECTION-C6videos
SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C6videos
SAMPLE PAPER 5
Similar Questions
Consider the motion of a charged particle of mass m and charge q moving with velocity →v in a magnitude field →B. If →v is perpendicular to →B, show that it describe a circular path having angular frequency ω=qBm
View Solution(a) Write the expression for the force →F acting on a particle of mass m and charge q moving with velocity →v in a magnetic field →B. Under what conditions will it move in (i) a circular path and (ii) a helical path?
(b) Show that the kinetic enery of the particle moving in magnetic field remains constant.View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m, charge e and velocity v moving in a magnetic field E perpendicular to the motion of particle. The radius of its path is:
ABemvBevBmCBvemDmvBe - Question 2 - Select One
A particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/Bq - Question 3 - Select One
A charged particle moves through a magnetic field perpendicular to its direction. Then
Akinetic energy changes but the momentum is constantBthe momentum changes but the kinetic energy is constantCboth momentum and kinetic energy of the particle are not constantDboth momentum and kinetic energy of the particle are constant
A charged particle moves through a magnetic field perpendicular to its direction. Then
View SolutionTwo particle A and B of masses mA and mB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then-
 View Solution
View SolutionTwo particles A and B of masses mAandmB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then -
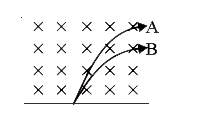 View Solution
View SolutionA charged particle is moving with velocity Vin magnetic field
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View Solution

