If 10μC charge exists at center of a square ABCD and 2μC point charge is moved form A to B. find the work done .
20 J
5 J
0
8 J
The correct Answer is:C
To solve the problem of finding the work done when a 2 µC charge is moved from point A to point B in the presence of a 10µC charge at the center of a square ABCD, we can follow these steps:
Step 1: Understand the Configuration
We have a square ABCD with a 10µC charge located at the center. The points A and B are at the corners of the square. We need to calculate the electric potential at points A and B due to the 10µC charge.
Step 2: Calculate the Distance from the Center to the Corners
The distance from the center of the square to any corner (A or B) can be calculated using the Pythagorean theorem. If the side length of the square is a, then the distance r from the center to a corner is:
\( r = \frac{a}{\sqrt{2}} \)
Step 3: Calculate the Electric Potential at Point A
The electric potential \( V_A \) at point A due to the 10µC charge is given by the formula:
\( V_A = \frac{k \cdot Q}{r} \)
Where:
- \( k \) is Coulomb's constant (\( 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \))
- \( Q = 10 \, \mu C = 10 \times 10^{-6} \, C \)
- \( r = \frac{a}{\sqrt{2}} \)
Substituting the values:
\( V_A = \frac{9 \times 10^9 \cdot 10 \times 10^{-6}}{\frac{a}{\sqrt{2}}} = \frac{9 \times 10^9 \cdot 10 \times 10^{-6} \cdot \sqrt{2}}{a} \)
Step 4: Calculate the Electric Potential at Point B
Using the same reasoning as for point A, the electric potential \( V_B \) at point B is also:
\( V_B = \frac{k \cdot Q}{r} \)
Since point B is also at the same distance from the center as point A, we find:
\( V_B = V_A \)
Step 5: Calculate the Work Done
The work done \( W \) in moving the charge \( q \) from point A to point B is given by:
\( W = q \cdot (V_B - V_A) \)
Substituting the values:
\( W = 2 \times 10^{-6} \cdot (V_B - V_A) \)
Since \( V_B = V_A \):
\( W = 2 \times 10^{-6} \cdot (0) = 0 \)
Conclusion
The work done in moving the 2µC charge from point A to point B is:
\( W = 0 \, \text{J} \)
We have a square ABCD with a 10µC charge located at the center. The points A and B are at the corners of the square. We need to calculate the electric potential at points A and B due to the 10µC charge.
The distance from the center of the square to any corner (A or B) can be calculated using the Pythagorean theorem. If the side length of the square is a, then the distance r from the center to a corner is:
\( r = \frac{a}{\sqrt{2}} \)
The electric potential \( V_A \) at point A due to the 10µC charge is given by the formula:
\( V_A = \frac{k \cdot Q}{r} \)
Where:
- \( k \) is Coulomb's constant (\( 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \))
- \( Q = 10 \, \mu C = 10 \times 10^{-6} \, C \)
- \( r = \frac{a}{\sqrt{2}} \)
\( V_A = \frac{9 \times 10^9 \cdot 10 \times 10^{-6}}{\frac{a}{\sqrt{2}}} = \frac{9 \times 10^9 \cdot 10 \times 10^{-6} \cdot \sqrt{2}}{a} \)
Using the same reasoning as for point A, the electric potential \( V_B \) at point B is also:
\( V_B = \frac{k \cdot Q}{r} \)
Since point B is also at the same distance from the center as point A, we find:
\( V_B = V_A \)
The work done \( W \) in moving the charge \( q \) from point A to point B is given by:
\( W = q \cdot (V_B - V_A) \)
Substituting the values:
\( W = 2 \times 10^{-6} \cdot (V_B - V_A) \)
Since \( V_B = V_A \):
\( W = 2 \times 10^{-6} \cdot (0) = 0 \)
The work done in moving the 2µC charge from point A to point B is:
\( W = 0 \, \text{J} \)
Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
Similar Questions
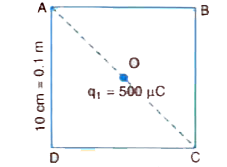
A 500 μ C charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10 μ C between two diagonally opposite points on the square.
View SolutionA charge of 60n C (nanocouloumb) is palced at the corner A of a square ABCD is side 10cm. Another charge of -10nc is located at the centre of the square. Find the work done in carrying a charge of +5 nC from the corner C to the corner B of square.
View Solution
Knowledge Check
If 10μC charge exists at center of a square ABCD and 2μC point charge is moved form A to B. find the work done .
A20 JB5 JC0D8 JIf 10μC charge exists at centre of a square ABCD and 2μC point charge is moved from A to B. Find the work done
A20JB5JC0D8JA charge of 10μC lies at the centre of a square. Work done in carrying a charge of 2μC from one corner of square to the diagonally opposite corner is
A20JB5JCZeroD20μJ
A500μC charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10μC between two diagonally opposite points on the square.
View SolutionA charge of 5μC is placed at the center of a square ABCD of side 10cm. Find the work done (inμJ) in moving a charge of 1μC from A to B.
View SolutionFour point charges qA=2μC,qB=−5μC,qC=−2μCandqD=−5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the square ?
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionFour point charges qA=2μC,qB=5μC,qC=2μCandqD=5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the centre of the square ?
(##U_LIK_SP_PHY_XII_C01_E01_006_Q01.png" width="80%">
View Solution
