A block of mass 8 kg is placed on a rough horizontal plane. A time dependent force F=kt2acts on the block, where k=3N/s2. Coefficient of friction is0.6. Force of friction between the block and the plane at t=1s is
48N
4N
2N
3N
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
- Mass of the block (m) = 8 kg
- Coefficient of friction (μ) = 0.6
- Time-dependent force (F) = kt², where k = 3 N/s²
- Time (t) = 1 s
Step 2: Calculate the force acting on the block at t = 1 s
Using the formula for the time-dependent force:
F=k⋅t2
Substituting the values:
F=3⋅(1)2=3N
Step 3: Calculate the maximum static friction (Fs_max)
The maximum static friction can be calculated using the formula:
Fsmax=μ⋅m⋅g
Where g (acceleration due to gravity) is approximately 10 m/s². Thus:
Fsmax=0.6⋅8⋅10=48N
Step 4: Compare the applied force and maximum static friction
Now we compare the applied force (3 N) with the maximum static friction (48 N):
- Since F<Fsmax (3 N < 48 N), the block will not move.
Step 5: Determine the force of friction acting on the block
Since the block does not move, the force of friction will equal the applied force to prevent motion:
Ffriction=F=3N
Final Answer:
The force of friction between the block and the plane at t = 1 s is 3 N.
---
- Mass of the block (m) = 8 kg
- Coefficient of friction (μ) = 0.6
- Time-dependent force (F) = kt², where k = 3 N/s²
- Time (t) = 1 s
Using the formula for the time-dependent force:
F=k⋅t2
Substituting the values:
F=3⋅(1)2=3N
The maximum static friction can be calculated using the formula:
Fsmax=μ⋅m⋅g
Where g (acceleration due to gravity) is approximately 10 m/s². Thus:
Fsmax=0.6⋅8⋅10=48N
Now we compare the applied force (3 N) with the maximum static friction (48 N):
- Since F<Fsmax (3 N < 48 N), the block will not move.
Since the block does not move, the force of friction will equal the applied force to prevent motion:
Ffriction=F=3N
The force of friction between the block and the plane at t = 1 s is 3 N.
Similar Questions
A block of mass 4kg is placed on a rough horizontal plane A time dependent horizontal force F=kt acts on the block (k=2N/s). Find the frictional force between the block and the plane at t=2 seconds and t=5 seconds (μ=0.2) .
View SolutionA block of mass 5kg is placed on a rough horizontal plane.A time dependent horizontal force F=(t2+2t) N acts on the block. The friction force between the block and the plane at t=3s is (μ=0.4)
View Solution
Knowledge Check
A block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
A32NB4NC2ND8NA block of mass 4kg is placed on a rough horizontal force plane. A time dependent horizontal force F=kt acts on the block. Here k=2Ns−1. The frictional force between the block and plane at time t=2s is (μ=0.2)
A4NB8NC12ND10NA block is placed on a rough horizontal plane. A time-dependent horizontal force F=kt2 acts on the block. Here k is a positive constant. Acceleration -time graph of the block is
A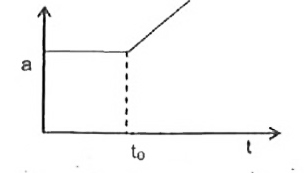 B
B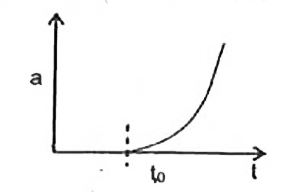 C
C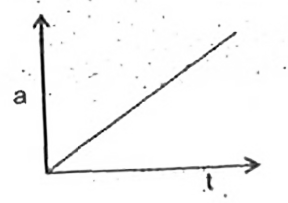 D
D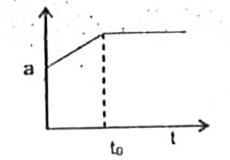
A block is placed on a rough horizontal plane. A time dependent horizontal force F=K t acts on the block K is a postive constant. Accelration-time graph of the block is
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View Solution
