The linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
mL
mL
mt2
mL3
The correct Answer is:A
Similar Questions
The linear mass density of the string shown in the figure is μ=1g/m. One end (A) of the string is tied to a prong of a tuning fork and the other end carries a block of mass M. The length of the string between the tuning fork and the pulley is L=2.0m. When the tuning fork vibrates, the string resonates with it when mass M is either 16 kg or 25 kg. However, standing waves are not observed for any other value of M lying between 16 kg and 25 kg. Assume that end A of the string is practically at rest and calculate the frequency of the fork.

View SolutionTransverse waves pass through the strings A and B attached to an object of mass m as shown. If μ is the linear density of each of the strings the velocity of the transverse waves produced in the strings A and B is
View Solution
Knowledge Check
The linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
AmLBmLCmL2DmL3The mass suspended from the stretched string of a sonometer is 4 kg and the linear mass density of string 4×10−3kgm−1 . If the length of the vibrating string is 100 cm , arrange the following steps in a sequential order to find the frequency of the tuning fork used for the experiment .
(A) The fundamental frequency of the vibratinng string is , n = 12l√Tm.
(B) Get the value of length of the string (l) , and linear mass density (m) of the string from the data in the problem .
(C) Calculate the tension in the string using , T = mg .
(D) Substitute the appropriate values in n=12l√Tm and find the value of 'n' .ABCADBABCDCDCBADBADCFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.

Find the time taken by wave to reach from source end to fixed end.A2512×L√F/μB10L√F/μC4L√F/μDL√F/μ
Four pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F. Find the time taken by wave to reach from source end to fixed end.

View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.

Find the ratio of wavelength of the wave on four string, starting from right hand side.
View SolutionMiddle C on a piano has a fundamental of 262Hz, and the first A above middle C has a fundamental frequency of 440Hz.
a. Calculate the frequencies of the next two harmonics of the C string .
b. If AandC, strings have the same linear mass density μ and length L, determine the ratio opf tensions in the two strings .
View SolutionTransverse waves pass through the strings A and B attached to an object of mass 'm' as shown. If μ is the linear density of each of the strings, the velocity of the transverse waves produced in the strings A and B is
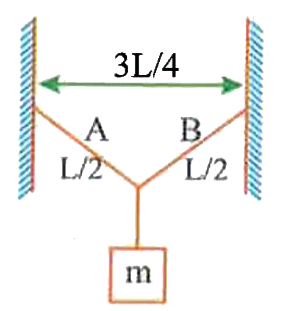
View SolutionOne end of a string of length l is tied to the ceiling of a lift accelerating upwards with an acceleration g/2. The linear mass density of the string is μ(x)=μ0x1/2 where, x is measured from the bottom. The time taken by a pulse to reach from bottom to top is
View Solution
