Two different conductors have same resistance at 0∘ C It is found that the resistance of the first conductor at t∘1 C is equal to the resistance of the second conductor at t∘2 C. The ratio of temperature coefficients of resistance of the conductors,a1a2 is
t1t2
t2−t1t2
t2−t1t1
t2t1
The correct Answer is:D
To solve the problem, we need to establish the relationship between the resistances of the two conductors at different temperatures and derive the ratio of their temperature coefficients of resistance.
1. Understanding the Given Information:
- Let the resistance of both conductors at 0∘C be R.
- The temperature coefficients of resistance for the first and second conductors are denoted as α1 and α2 respectively.
2. Resistance at Different Temperatures:
- The resistance of the first conductor at t∘1C can be expressed as:
R1=R(1+α1t1)
- The resistance of the second conductor at t∘2C can be expressed as:
R2=R(1+α2t2)
3. Setting Up the Equation:
- According to the problem, the resistance of the first conductor at t∘1C is equal to the resistance of the second conductor at t∘2C:
R(1+α1t1)=R(1+α2t2)
4. Cancelling the Resistance:
- Since R is the same for both conductors and is not zero, we can divide both sides by R:
1+α1t1=1+α2t2
5. Simplifying the Equation:
- By subtracting 1 from both sides, we get:
α1t1=α2t2
6. Finding the Ratio of Temperature Coefficients:
- Rearranging the equation gives us:
α1α2=t2t1
Final Result:
Thus, the ratio of the temperature coefficients of resistance of the two conductors is:
α1α2=t2t1
- Let the resistance of both conductors at 0∘C be R.
- The temperature coefficients of resistance for the first and second conductors are denoted as α1 and α2 respectively.
- The resistance of the first conductor at t∘1C can be expressed as:
R1=R(1+α1t1)
- The resistance of the second conductor at t∘2C can be expressed as:
R2=R(1+α2t2)
- According to the problem, the resistance of the first conductor at t∘1C is equal to the resistance of the second conductor at t∘2C:
R(1+α1t1)=R(1+α2t2)
- Since R is the same for both conductors and is not zero, we can divide both sides by R:
1+α1t1=1+α2t2
- By subtracting 1 from both sides, we get:
α1t1=α2t2
- Rearranging the equation gives us:
α1α2=t2t1
Thus, the ratio of the temperature coefficients of resistance of the two conductors is:
α1α2=t2t1
Similar Questions
The resistance of a conductor at 20∘Cis6.3Ωandat100∘C it is 7.5Ω . Calculate the resistance of the conductor at 0∘C and its temperature coefficient of resistance .
View SolutionVariation of resistance of the conductor with temperature is shown . Temperature coefficient of the conductor is
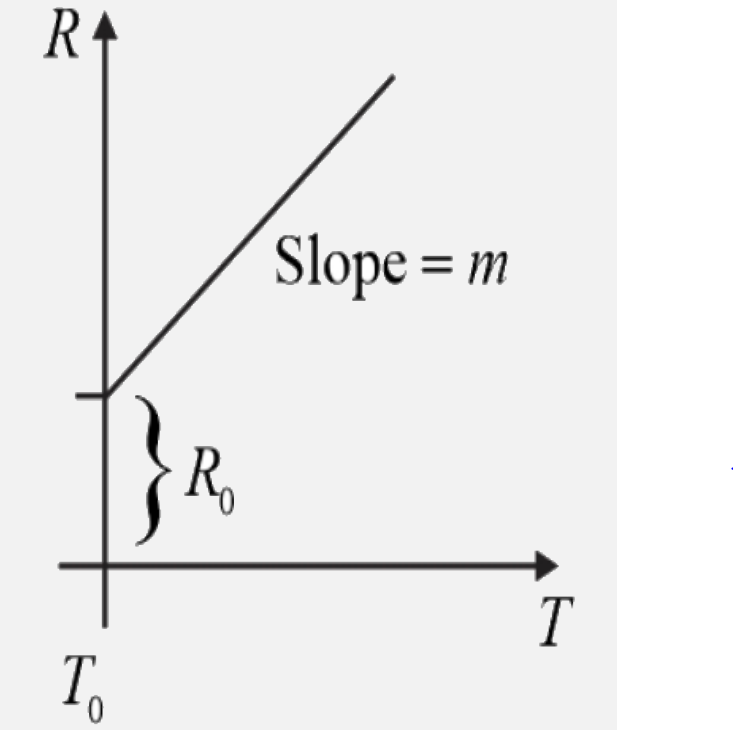 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The temperature coefficient of resistance of a conductor is
APositive alwaysBNegative alwaysCzeroDInfinite - Question 2 - Select One
The temperature coefficient of resistance of a semi conductor is
AIs always positiveBIs always negativeCIs zeroDMay be positive or negative or zero - Question 3 - Select One
The ratio of the resistances of a conductor at a temperature of 15∘C to its resistance at a temperature of 37.5∘C is 4:5. The temperature coefficient of resistance of the conductor is
A125.∘C−1B150.∘C−1C180.∘C−1D175.∘C−1
Why does resistance of a metallic conductor increase with increase in temperature?
View SolutionThe resistance of a conductor at 30∘C is 3.25Ω and at 100∘C is 3.95Ω. Calculate the temperature coefficient of resistance of the conductor and the resistance of the conductor at 0∘C.
View SolutionAs the temperature increases, resistivity of semi-conductor:
View SolutionIf the resistance of a conductor is 5Ω at 50∘C and 7Ω at 100∘C then the mean temperature coefficient of resistance of the material is
View SolutionThe resistance of a conductor at 15∘C is 16Ω and at 100∘C is 20Ω. What will be the temperature coefficient of resistance of the conductor ?
View Solution

