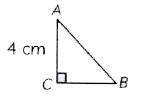
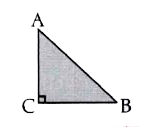
ABC is an isosceles triangle, which is right angled at B with AB = 4 cm. What is the length of AC?
2 cm
2√2 cm
4 cm
4√2 cm
The correct Answer is:D
Step by step video, text & image solution for ABC is an isosceles triangle, which is right angled at B with AB = 4 cm. What is the length of AC? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -5EXERCISE - SECTION-C11videos
SAMPLE PAPER -5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -5EXERCISE - SECTION-C11videos
SAMPLE PAPER -5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 3EXERCISE - SECTION-C10videos
SAMPLE PAPER - 3
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -6 EXERCISE - Part - B (Section - V)6videos
SAMPLE PAPER -6
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ?
A4 cmB6 cmC7 cmD5 cm - Question 2 - Select One
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cm - Question 3 - Select One
ABC is triangle right angled at B. If AB = 6 cm and BC= 8 cm, then what is the length of the circum- radius of the ΔABC ?
A10 cmB7 cmC6 cmD5 cm
In figure below ABC is an isosceles triangle right at C with AC =4 cm . Find the length of AB .
View SolutionABC is an isosceles triangle in which AB=ACand(∠A)=2(∠B)AB=4cm. What is the ratio of inradius to the circumradius?
View SolutionABC is an isosceles triangle right-angled at C. Prove that AB2=2AC2.
View SolutionABC is an isosceles triangle such that AB=BC=8cm and ∠ABC=90∘ What is the length of the perpendicular drawn from B to AC?
View SolutionABC is a triangle right angled at B. If AB=5 cm and BC= 10 cm, then what is the length of the perpendicular drawn from the vertex B to the hypotenuse ?
View Solution