If V is the real vector space of all mapping from R to R V1={fsiVf(−x)=f(x)} and V_2={fsiV/f(-x) =-f(x)} then which one of the following is correct?
Neither V1 nor V2 is a subspace of V
V1 is a subspace of V but V2 is npt a subspace of V
V1 is not a subspace of V but V2 is a subspace of V
BothV1 and V2 are subspace of V
The correct Answer is:D
Similar Questions
Knowledge Check
- Question 1 - Select One
If V is the vector space of all functions from R to R and W={f:f(4)=3+f(2)}
AW is a subspace of VBW is not a subspace ofVCW is not closed under scalar multiplicationDW is closed under scalar multiplication - Question 2 - Select One
If V is the vector space of all functions from R TO R and W={f:f(5)=0}
AW is a subspace of VBW is not a subspace ofVCW is closed under multiplicationDW is not closed under multiplication - Question 3 - Select One
If V be the vector spacce of all functions from R to R and W-{f:2f(3)=f(1)}
AW is a subspace of VBW is not a subspace ofVCα+βsiW⇒α+βsiwDα+βsiW⇒α+3βsiw
The composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
View SolutionLet f:R→R be a function such that f(x+y)=f(x)+f(y)for all,x,y∈R
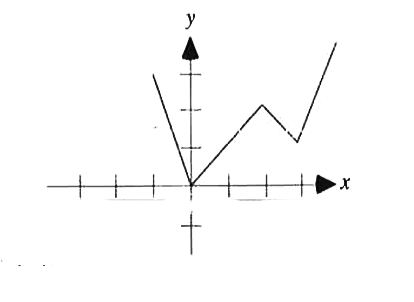
If f(x) is differentiable at x=0. then, which one of the following is incorrect?View SolutionThe graph of y=f(x) is shown to the right. If f(−1)=v, then which one of the following could be the value of f(v) ?
 View Solution
View SolutionLe f:R→Randg:R→R be functions satisfying f(x+y)=f(x)+f(y)+f(x)f(y)andf(x)=xg(x) for all x,y∈R.Iflimx→0g(x)=1 , then which of the following statements is/are TRUE ?
View SolutionLet R be the set of real number and f:R→R be given by f(x)=√|x|−log(1+|x|). We now make the following assertions :
I. There exists a real number A such that f(x)≤A for all x.
II. There exists a real number B such that f(x)≥B for all x.View Solution

