Find the centre of mass of three particles at the vertices of an equilateral triangle .The masses of the particles are 100 gram, 150 gram and 200 gram respectively .Each side of the equilateral triangle is 0.5 m long.
Length of side =0.5 m
mass m1=100 g
m2=150gandm3=150 g
distances x1=0,y1=0,
x2=0.5,y2=0
x3=0.25,y3=0.25√3
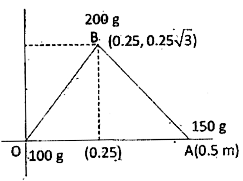
Centre of mass Xcm=m1x1+m2x2+m3x3m1+m2+m3
=0+150×(0.5)+200×0.25100+150+200
Xc.m=75+50450=125450=518m
Yc.m=m1y1=m2y2+m3y3m1+m2+m3
=100+0+150×0+200×0.25√3450
50√3450=√39=13√3m.
Topper's Solved these Questions
- MODEL PAPER 4 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 4 EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 4 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 4 EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 3 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 3 EXERCISE - SECTION-C
3 Videos
- MODEL PAPER 5BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 5EXERCISE - SECTION - C
3 Videos
Similar Questions
Find the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g,150g,and200g respectively. Each side of the equilateral triangle is 0.5m along.
View SolutionFind the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g,150g,and200g respectively. Each side of the equilateral triangle is 0.5m along.
View Solution
Knowledge Check
The centre of masses of three particles of mass m1=m2=m3=1 kg at the corners of an equilateral triangle of side 1 m will be -
A0.50m, 0.29mB0.43m, 0.50mC0.25m, 0.25mD0.22m, 0.22mThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3LThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?AMoment of inertia about axis '1' is 54ml2BMoment of inertia about axis '2' is 34ml2CMoment of inertia about an axis passing through one corner and perpendicular to the plane is 2ml2DAll of these
Find centre of mass of a system of three particle kept at the corner equilateral triangle as shown in figure
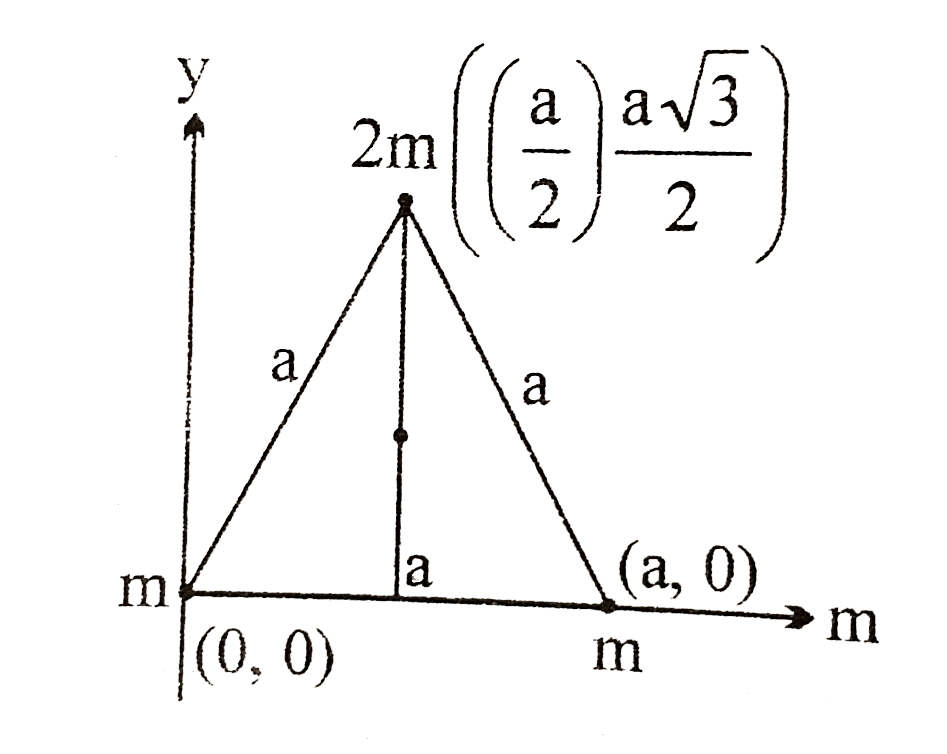
View SolutionThree particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionWork done by an external agent in bringing three particles each of mass m at the vertices of an equilateral triangle of length l is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution
