Question

Show that the motion of a simple pendulum is simple harmonic and hence, derive an equation for its time period. What is the length of a simple pendulum, which ticks seconds ?

Explanation

Simple pendulum : In a laboratory a heavy metallic bob is suspended from a rigid support with the help of a spunless thread. This arrangement is known as simple pendulum.
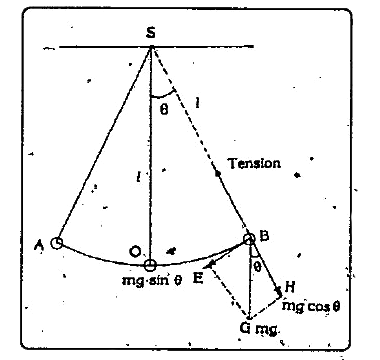
Let the length of simple pendulum is .l. and the point of suspension is .S.. Let the pendulum is drawn to a side by a small angle `.theta.` and allowed free to oscillate in the vertical plane. Then it will oscillate between the extreme positions A and B with a displacement say .x. at any given time.
Let the bob is at one extreme position say B. The force vertically acting downwards is weight W = mg.
By resolving the weight into two perpendicular components :
1. The component mg sin `theta` is responsible for the to and for motion of the bob.
2. The component mg cos `theta` will balance the tension in the string. Force useful for motion F = mg sin `theta` = ma (From Newton.s 2nd Law)
`therefore a = g sin theta`

When `theta` is small `sin theta ~~ theta = ("arc")/("radius") = (x)/(l)`
`therefore a = g(x)/(l)" "...(1) or a prop x`
Since acceleration is proportional to displacement and acceleration is always directed towards a fixed point the motion of simple pendulum is simple harmonic.
Time period of simple pendulum :
Time period of a body in S.H.M `= 2pi sqrt((Y)/(a)) = 2pi sqrt(("displacement")/("acceleration"))`
From equation (1) `a = (g)/(l) x or (x)/(a) = ("displacement (y)")/("acceleration (a)") = (l)/(g)`
`therefore` Time period of simple pendulum, `T = 2pi sqrt((Y)/(a)) = 2pi sqrt((l)/(g))`
Problem :
In pendulum `g = 4 pi^(2) (l)/(T^(2))` put g = 10 `m//sec^(2)` (Nearly)
`pi^(2) = 10` (Nearly), For seconds pendulum T = 2 sec
But `l = g T^(2)//4 pi^(2) = (10 xx 4)/(4 xx 10) = 1m`
`therefore` Length of seconds pendulum on earth = 1m = 100 cm (nearly).