Question

Activate Windows Go to PC settings to activate Wine Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. Find the length of a simple pendulum which ticks seconds. $(g=9.8m{s}^{-2})$

Explanation

Simple pendulum : In a laboratory, a heavy metallic bob is suspended from a rigid support with the help of a spunless thread. This arrangement is known as simple pendulum
Let the length of simple pendulum is .l and the point of suspension is .S.. Let the pendulum is drawn to a side by a small angle `theta` and allowed free to oscillate in the vertical plane. Then It will oscillate between the extreme positions A and B with a displacement say .x. at any given time,
Let the bob is at one extreme position say B. The force vertically acting downwards is weight W =mg.

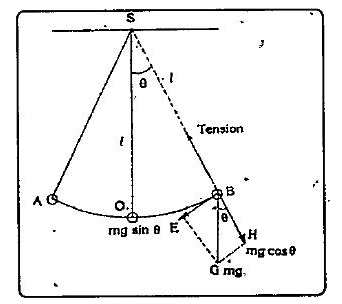
By resolving the weight into two perpendicular components
1) The component mg sin `theta` is responsible for the to and fro motion of the bob.
2) The component mg cos `theta` will balance the tension in the string.
Force useful for motion F = mg sin `theta ` = ma ( From Newton.s 2nd Law )
`:. a = g sin theta `
When ` theta ` is small sin ` theta ~~ theta = ("arc ")/( "radius ") = (x)/(l)`
`:. a = g (x)/( l)` . . . . . . . (1) or ` a prop x `
Since acceleration is proportional to displacement and ac celeration is always directed towards a fixed point the motion of simple pendulum is simple harmonic.
Time period of simple pendulum :
Time period of a body in S.H.M
` 2 pi sqrt(( y)/( a)) = 2 pi sqrt(( " displacement ")/( " acceleration ")) `
From equation (1) ` a = (g)/(l) xx ` or ` (x)/( a) ("displacement (y)")/( "acceleration (a)") = (l) /(g)`
`:.` Time period of simple pendulum ` t = 2 pi sqrt(( y)/( a)) = 2 pi sqrt(( l)/( g))`
Problem :
In simple pendulum ` T = 2 pi sqrt( (l)/( g))` or `l ( g t^(2))/( 4 pi ^(2))`
For seconds pendulum ` T = 2 s rArr t^(2) = 4 `
` :. l = (9 . 8 xx4)/( 4 pi ^(2))` = 1 m (` :. pi^(2) nearly 9 . 8` )