Question

Explain the formation of stationary waves in stretched strings and derive harmonic equations.

Explanation

Stationary wave : Two progressive waves of same wavelength, amplitude and frequency travelling in opposite directions super impose over each other produce stationary waves or standing wave.
Formation of stationary wave in a stretched string:
Let us consider a string of length .I stretched at the two fixed ends .A. and .B..
Now pluck the string per pendicular to its length

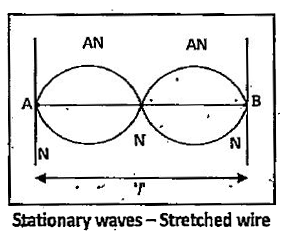
The transverse wave travel along the length of the string and get reflected at fixed ends.
Due to superimposition of these reflected waves, stationary waves are formed in the string.
Equation of Stationary Wave : Let two transverse progressive waves with the same amplitude .A., wavelength and frequency .n., travelling in opposite direction along a stretched string be. given by
`y_(1)=A sin (kx- omegat) and y_(2)=A sin (kx+omegat)`
where `omega=2pi n and k=(2pi)/(lambda)`
Applying the principle of superposition of waves, the resultant wave is given by
`y=y_(1)+y_(2)`
`y=A sin (kx- omegat)+A sin (kx+omegat)`
`y=2A sin kx cos omegat`
Amplitude of resultant wave `(2A sin kx)` is no more constant.
It depends on the value of kx. When `x=0, (lambda)/(2),(2lambda)/(2),(3lambda)/(2)`..... etc
The amplitude becomes zero.
hese positions of zero amplitude are known as "Nodes", when `x=(lambda)/(4),(3lambda)/(4),(5lambda)/(4)`.... tc the amplitude becomes 2A (Maximum).
These positions of maximum amplitude are known as "Antinodes".
Equation of fundamental frequency : If the wire of length .l is stretched between points .A. and .B. with tension T vibrates as a single loop then the frequency of the vibrations is known as fundamental frequency and is denoted by .u.
Then length of the wire is equal to `(lambda)/(2)`
But velocity of a wave `v=u lambda -(1)`
In case of stretched strings `v= sqrt(T//mu)=-(2)`
Where v is the velocity of transverse vibrations in the string.
T is the tension,
`mu` is the linear density of the string.
From above equation `u=(1)/(lambda) sqrt(T//mu)`
For fundamental `lambda2=l. :. v=(1)/(2l) sqrt((T)/(mu))`
If the wire vibrates for p loops then the frequency is given by `v_(p)=(p)/(2l) sqrt((T)/(mu))`
Formation of harmonics in stretched wires : From above equation if the wire vibrates with one loop then p =1
Frequency of 1st harmonic `v_(1)=(1)/(2l) sqrt((T)/(mu))`

For frequency of 2nd, harmonic put `p=2u_(1)(2)/(l) sqrt((T)/(mu))`


For frequency of 3rd harmonic put p= 3,
Frequency of 3rd harmonic `u_(3)=(3)/(2l) sqrt((T)/(mu))`