What is Doppler effect? Obtain an expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest.
A train sounds its whistle as it approaches and crosses a level crossing. An observer at the crossing measures a frequency of 219 Hz as the train approaches and a frequency of 184 Hz as it leaves. If the speed of sound is taken to be 340 m/s, find the speed of the train and the frequency of its whistle.

Text Solution

Verified by Experts

Doppler effect: The apparent change in the frequency of the source of sound due to relative motion between the observer and the source of sound is called "Doppler effect".
Derivation for apparent frequency when source is in motion and observer at rest : Let .s. is a source of sound moving with a velocity $v_{s}$ away from a stationary observer. Let the source produces a sound of frequency $v_{0}$ and its time period is $T_{0}$ . Let the medium in which source is moving is at rest. Let the observer has some device to count the number of crests compressions of wave produced.
At time t = 0 the source produces a crest. Let the distance between source and observer is .L. and velocity of sound is .v..

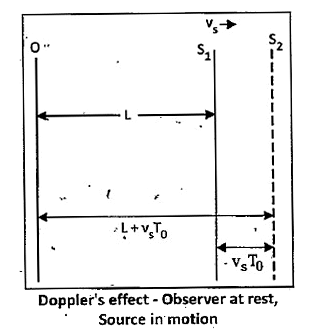
Now time taken by observer to detect crest = $t_{1} = \frac{L}{v} \to 1$
The second crest is produced after a time interval $T_{0}$
During this time the source will travel a distance of $v_{s} T_{0}$ . So total distance from observer = $L + v_{s} T_{0}$
Time Taken to detect 2nd crest = $t_{2} = T_{0} + [\frac{L + v_{s} T_{0}}{v}] \to 2$
Let the source produced (n+1)th crest at time $n T_{0}$
Now time taken to detect that crest= $t_{n + 1} = n T_{0} + [\frac{L + n T_{0} v_{s}}{v}]$
TIme gap recorded n crests $= t = t_{n + 1} - t_{1}$
$= n T_{0} + [\frac{L + n T_{0} v_{s}}{v} - \frac{L}{V}] \to 3$
Time period of wave recorded by observer $T = \frac{total time(t)}{number of crests (n)}$
$∴ T = [n T_{0} + \frac{L + n v_{s} T_{0}}{v} - \frac{L}{v}] / n$
$∴ T = [n T_{0} + \frac{L}{v} + \frac{n v_{s} T_{0}}{v} - \frac{L}{v}] / n$
$= T_{0} + \frac{v_{s} T_{0}}{v} = T_{0} (1 + \frac{v_{s}}{v}) \to$ 4
But frequency $v = \frac{1}{T} and v_{0} = \frac{1}{T_{0}}$
$∴ \frac{1}{v} = \frac{1}{v_{0}} (1 + \frac{v_{s}}{v}) O R v = v_{0} {(1 + \frac{v_{s}}{v})}^{- 1}$
On binomial expansion and dropping of higher terms
${[1 + \frac{v_{s}}{v}]}^{- 1} = (1 - \frac{v_{s}}{v})$
$∴ v = v_{0} (1 - \frac{v_{s}}{v}) or v = v_{0} (\frac{v - v_{s}}{v})$
So apparent frequency $v < v_{0}$
If source is moving towards observer then $v_{s}$ is -ve (as per sign convension)
$∴$ apparent frequency $v = v_{0} [1 - \frac{(- v_{s})}{v}] = v_{0} (1 + \frac{v_{s}}{v})$
When source is approaching the observer frequency heard $v = v_{0} (\frac{v + v_{s}}{v}) O R v = v_{0} (1 + \frac{v_{s}}{v})$ . In this case apparent frequency heard $v > v_{0}$
Problem: Speed of sound in air $v = 340 m s^{- 1}$
Apparent frequency heard by observer when train approaches $v . = 219 H z$
$v = n (\frac{v}{v - v_{s}}) \Rightarrow 219 = n (\frac{340}{340 - v_{s}}) \to 1$
When train leaves the observer apparent frequency n..= 184Hz
$v . . = v (\frac{v}{v + v_{s}}) \Rightarrow 184 = n (\frac{340}{340 + v_{s}}) \to$ (2)
Divide (1) and (2) $\frac{219}{184} = \frac{340 + v_{s}}{340 - v_{s}} \Rightarrow v_{s} = 29.5 m s^{- 1}$
(b) from eq (1) $219 = n (\frac{340}{340 - 29.5})$
$∴ n = \frac{219 \times 310.5}{340}, n = 200 H z$

Updated on:21/07/2023

An observer standing at station observes frequency $219 H z$ when a train approaches and $184 H z$ when train goes away from him. If velocity of sound in air is $340 m / s$ , then velocity of train and actual frequency of whistle will be
A $15.5 m s_{1}, 200 H z$
B $19.5 m s^{- 1}, 205 H z$
C $29.5 m s^{- 1}, 200 H z$
D $32.5 m s^{- 1}, 200 H z$
A man standing on a platform observes that the frequency of the sound of a whistle emitted by a train drops by 140 Hz. If the velocity of sound in air is 330 m/s and the speed of the train is 70 m/s, the frequency of the whistle is
A571 Hz
B800 Hz
C400 Hz
D260 Hz
A man standing on a platform observes that the frequency of the sound of a whistle emitted by a train drops by 140 Hz. If the velocity of sound in air is 330 m/s and the speed of the train is 70 m/s, the frequency of the whistle is
A571 Hz
B800 Hz
C400 Hz
D260 Hz