Question

State-Kirchhoff's laws for an electrical network. Using these laws deduce the conditions for balance in a Wheatstone bridge. A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter ?

Explanation

Kirchhoff.s Laws :
i) Junction rule : At any junction sum of currents entering the junction is equals to sum of currents leaving the junction. (OR) Alzebraic sum of currents around a junction is zero.
ii). Loop rule :-Alzebraic sum of changes in potential around any closed loop.involving resistors and cells in the loop is zero.
Applying Kirchhoff.s Law to Wheatstones bridge:

Wheatstone Bridge Wheatstones bridge consists of four resistances P, Q, R, S connected, as shown in the figure and are referred as arms of the bridge.
A battery of emf .E. is connected between two junctions A and Banda galvanometer of resistance .G. is connected between .C. and .D..
Applying Kirchhoff.s first law,
at the junction `C,i_(1)+i_(g)......(1)`
at the junction `D,i_(2)+i_(g)=i_(4)......(2)`
Applying Kirchhoff.s second law for the-loop ACDA
`-i_(1)P-i_(g).G+i_(2)R=0" ".......(3)`
For the loop CBDC,
`-i_(3)Q+i_(4)S+i_(g)G=0" ".......(4)`
If no current passes through the galvanometer then the bridge is said to be balanced:
So `i_(g)=0` then (1) (2) ,(3) and (4) becomes
`i_(1)=i_(3),i_(2)=i_(4),i_(1)P=i_(2)R` and `i_(3)Q=i_(4)S`.
By adjusting the above equations we get `(P)/(Q)=(R )/(S)`.
This is the balancing conditions of a Wheatstones bridge.
Problem:
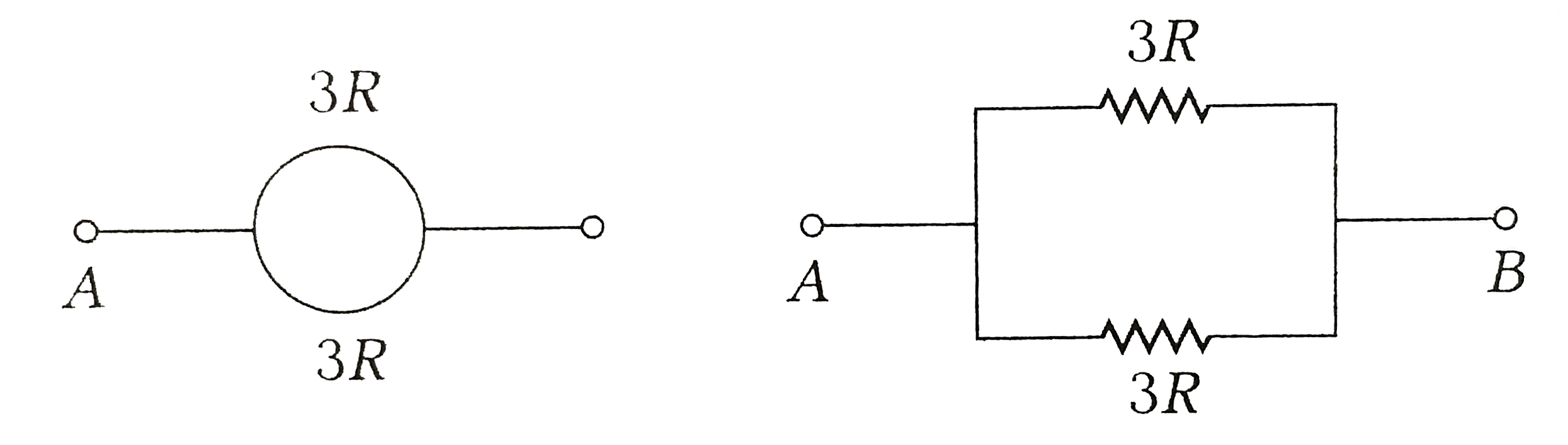
Resistance = 4R
The wire is bent in the form of a circle and Resistance is to be calculated along its diameter.

Between the point AB the wire is a parallel combination of 2R and 2R.
`:.` Resultant resistance `(1)/(R_(R))=(1)/(2R)+(1)/(2R)=(1)/(R)`.
`:.` Effective resistance between A & B =.R.