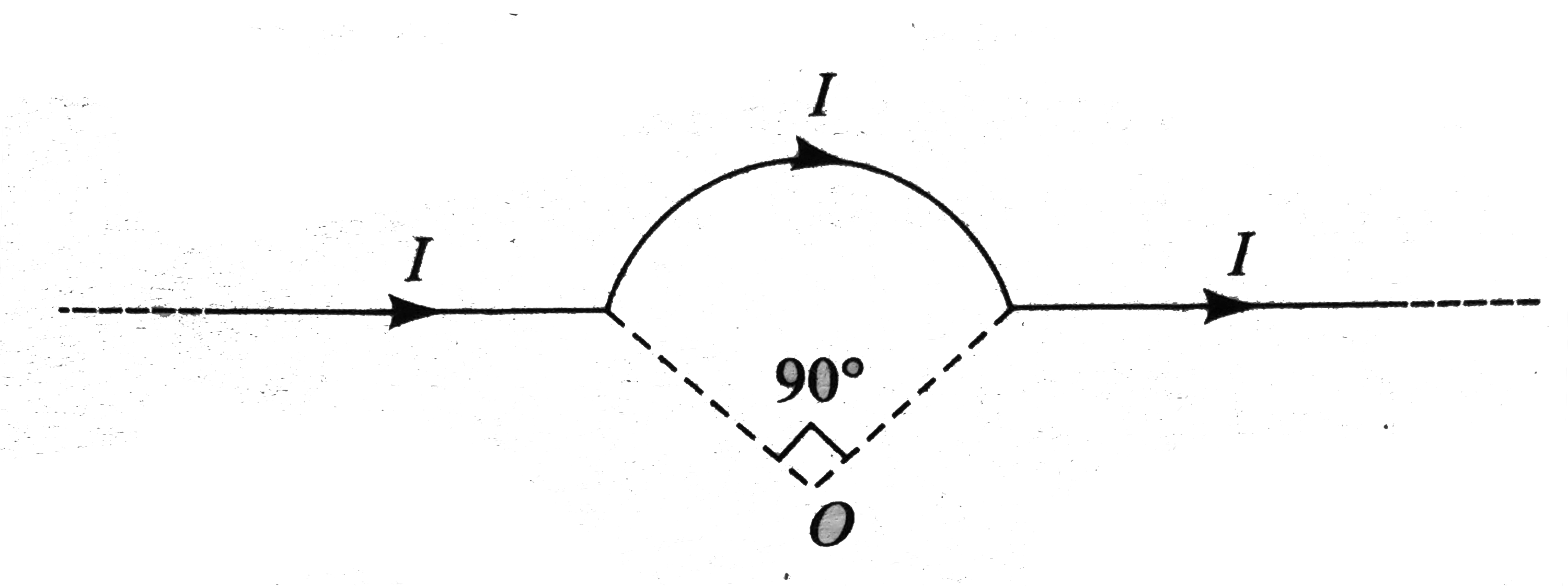
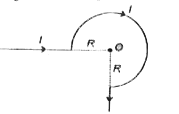
Study the current distribution given in the figure and calculate the magnetic field at the centre O .

OP=r,OQ=2r
A
μ0I24r
B
3μ0I24r
C
13μ0I24r
D
9μ0I24r
Text Solution
The correct Answer is:D
The magnetic field at a point due to a circle arc is given by,
B=μ0iθ4πr
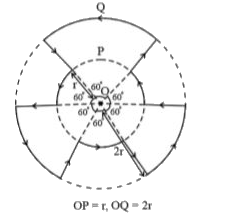
OP=r,OQ=2r
The magnetic field at the centre will be due to the three circular acros of radius r and radius 2 r.
The magnetic field due to the arcs of radius r will be equal to
B1=3(μ0i4πr×π3)
The magnetic field due to the arcs of radius 2 r will be equal to,
B2=3(μ0i4π2r×π3)
→Bnet=→B1+→B2
we get the direction of magnetic by Right-Hand Screw Rule, The direction of B1andB2 are outside the plane
Bnet=⎛⎜⎝μ0Iμ0I+4r8r⎞⎟⎠=3μ0I8r
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given loop the magnetic field at the centre O is
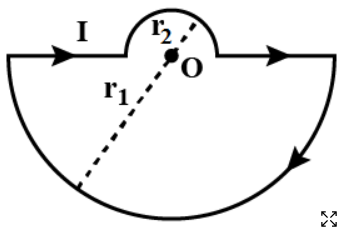 AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the page
AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the pageThe magnetic field at the centre of semicircle o in the figure is
 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)The magnetic field at the centre of semicircle o in the figure is
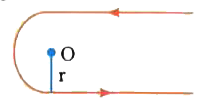 AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
AB=μ0i4rBμ0i4r(1+2π)Cμ0i4πr(π−2)Dμ0i4πr(π+2)
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionThe magnetic field at the centre O of the are shown in the figure is

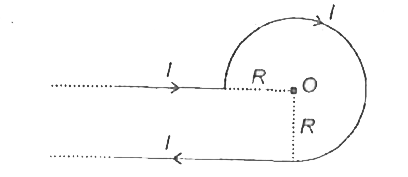
View SolutionMagnetic field at the centre O due to the given structure is
View SolutionMagnetic field at the centre O due to the given structure is
View Solution