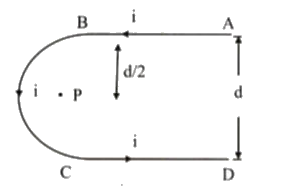
AB and CD are straight wires and BC (curved) is a semicircle. A current 'i' is passed through it. Let the magnetic field due to all three segments at point P(centre of semicircle) be Q μ0id. What is the value of Q?
The correct Answer is:00.82
Magnetic field due to AB
B1=12×μ0i2π(d2)=μ0i2πd out of plane
Magnetic field due to CD,
B2=12×μ0i2π(d2)=μ0i2πd out of plane
Bnet=B1+B2+B3......[∴ all in same directions]
=μ02d[1+2π]
=0.82μ0id
Topper's Solved these Questions
Similar Questions
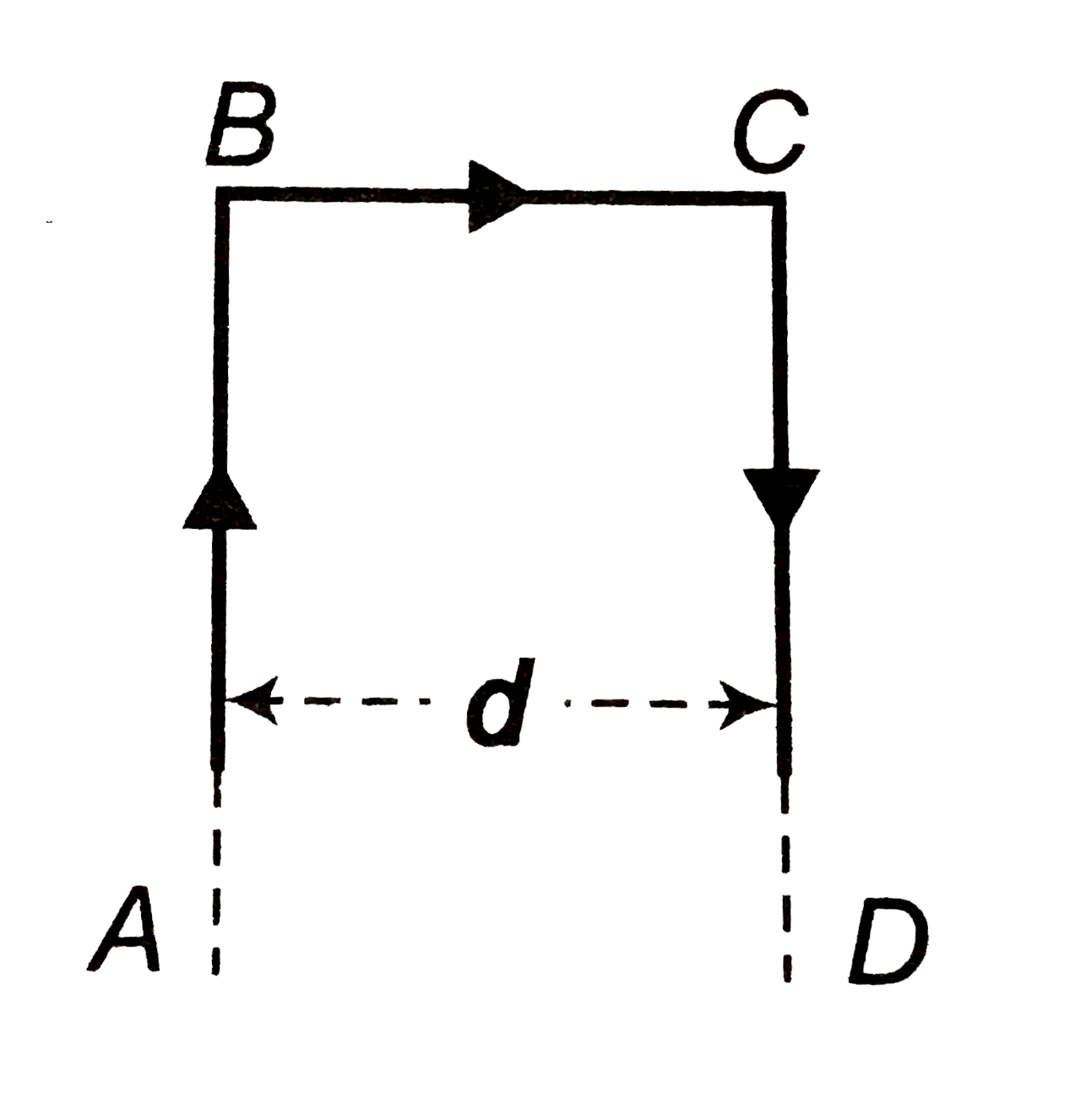
AB and CD are long staright conductors, distance d apart, carrying a current I. The magnetic field on BC due to the currents in AB and CD
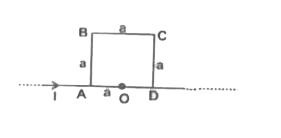
View SolutionThe resistance per unit length of the wires in segments AB, BC, CD, and AD are the same. The magnetic field due to the current at point O is
View Solution
Knowledge Check
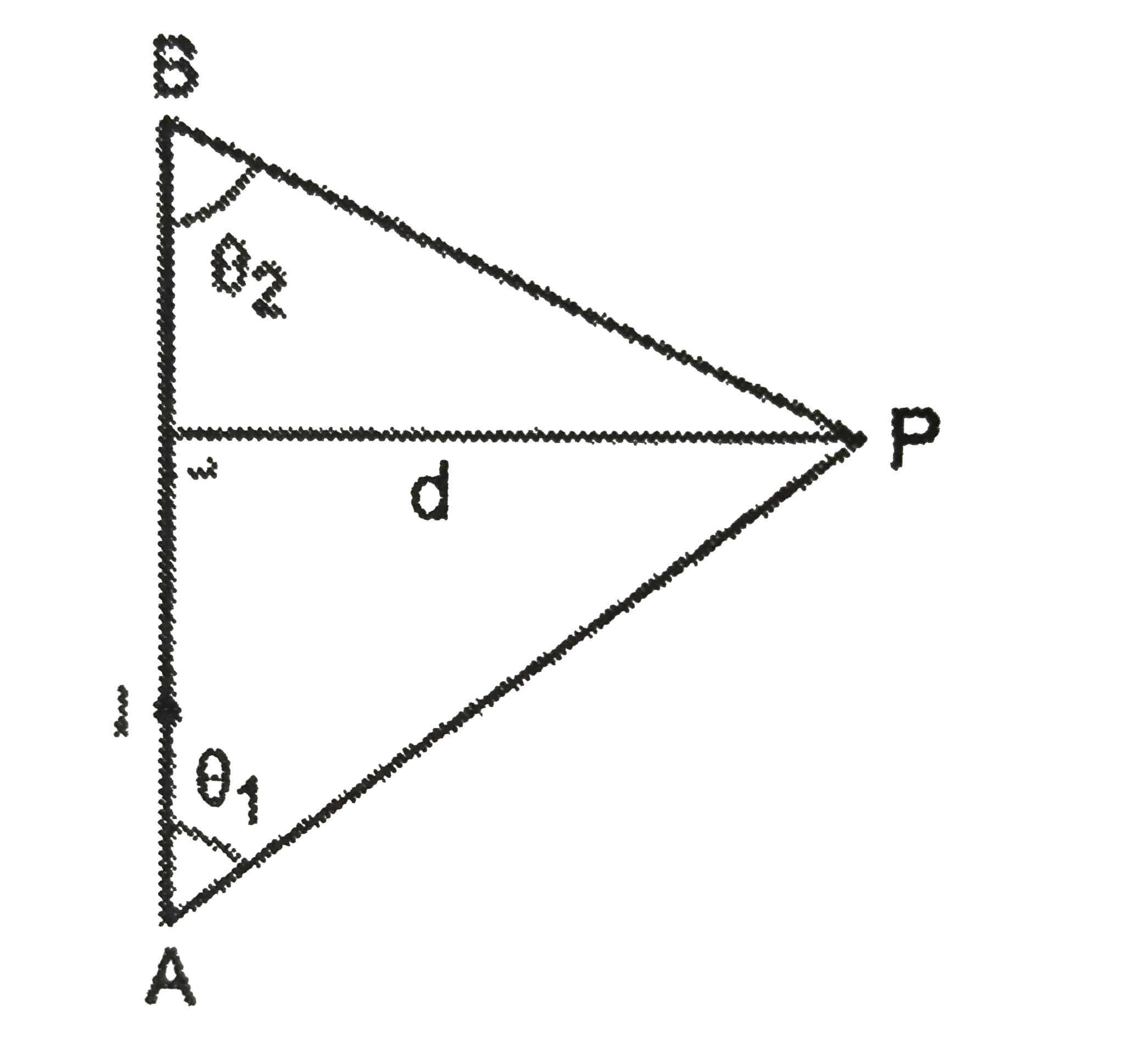
AbB is a section of a straight wire carrying a current I. P is a point at a distance d from AB. The magnetic field at P due to AB has magnitudeAμ0I4πd(cosθ1+cosθ2)Bμ0I4πd(cosθ1−cosθ2)Cμ0I4πd(sinθ1+sinθ2)Dμ0I4πd(sinθ1−sinθ2)AB and CD are long staright conductors, distance d apart, carrying a current I. The magnetic field on BC due to the currents in AB and CD
 Ais zero at all pointsBis zero at this midpointChas different magnitudes at different pointsDis maximum at its midpoints
Ais zero at all pointsBis zero at this midpointChas different magnitudes at different pointsDis maximum at its midpointsAB and CD are long straight conductor, distance d apart, carrying a current I. The magnetic field at the midpoint of BC is
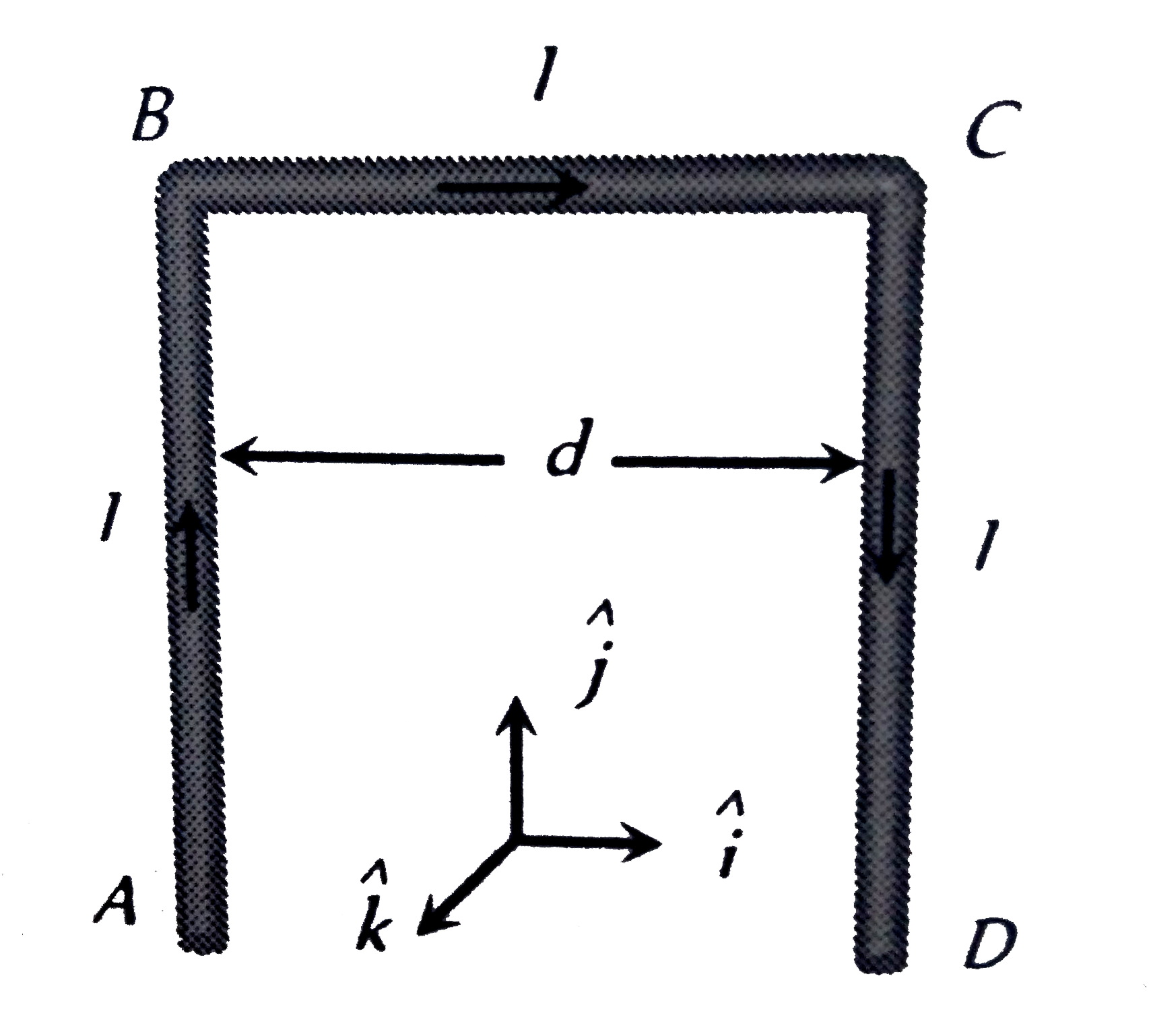 A−μ0I2πdˆkB−μ0IπdˆkC−μ0I4πdˆkD−μ0I8πdˆk
A−μ0I2πdˆkB−μ0IπdˆkC−μ0I4πdˆkD−μ0I8πdˆk
A hairpin like shape as shown in figure is made by bending a long current carrying wire. What is the magnitude of a magnetic field at point P which lies on the centre of the semicircle ?
View SolutionA straight wire carrying a current of 12A is bent into a semicircular arc of radius 2⋅0cm as shown in figure. Consider the magnetic field →B at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to →B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure

View SolutionA current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
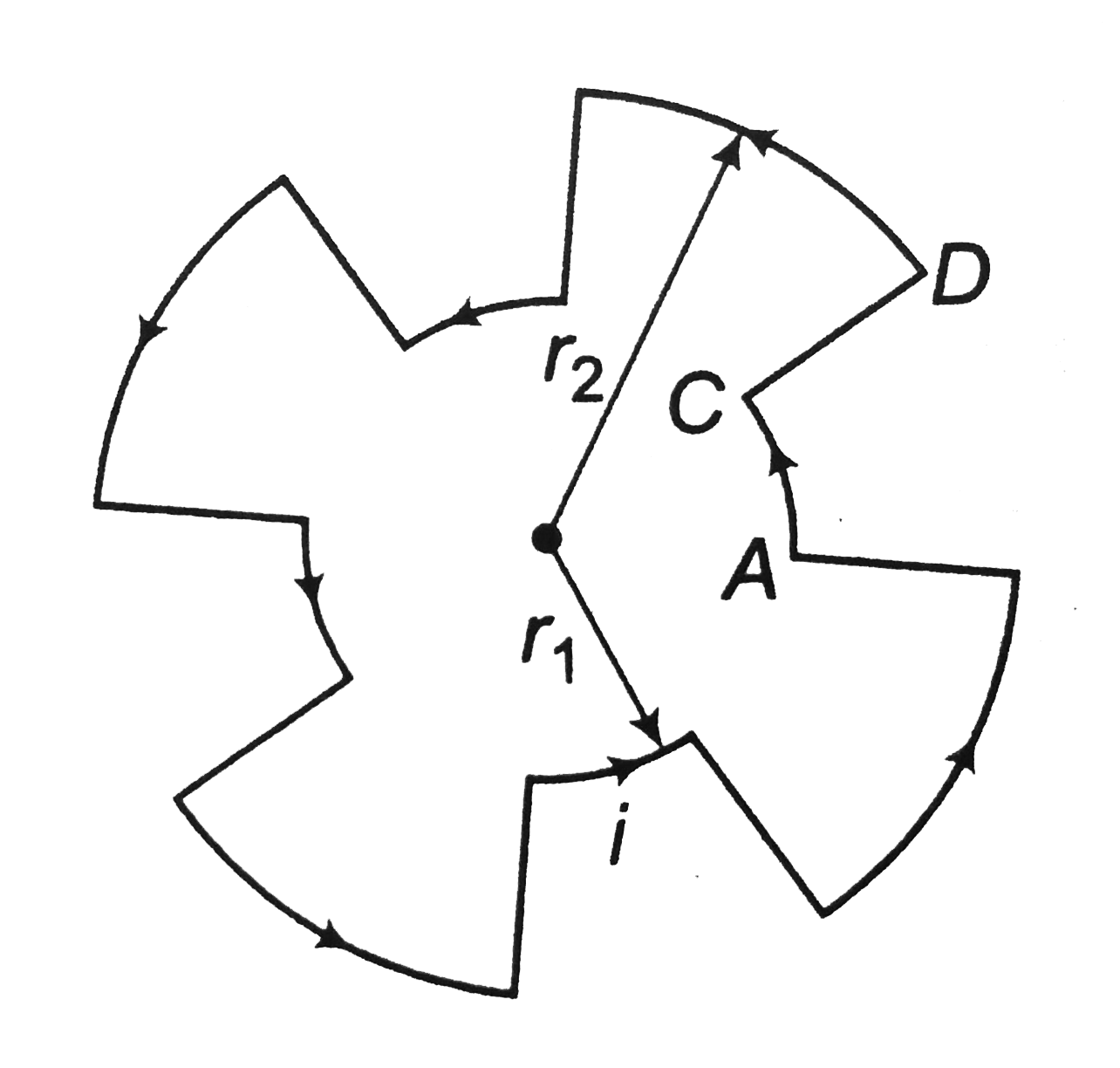
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionThe resistance per unit length of the wires in segments AB, BC, CD, and AD are the same. The magnetic field due to the current at point O is

View SolutionA conductor has three segments, two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?

View Solution
