The sum of two forces $\to P$ and $\to Q$ is $\to R$ such that $∣ ∣ \to R ∣ ∣ = ∣ ∣ \to P ∣ ∣$ . The angle $θ$ (in degrees) that the resultant of $2 \to P$ and $\to Q$ will make with $\to Q$ is , _____________.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:90

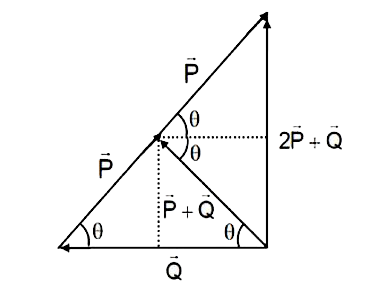
So angle between $(2 \to P + \to Q)$ is $90^{\circ}$
$∣ ∣ \to P + \to Q ∣ ∣ = ∣ ∣ \to P ∣ ∣$
$P^{2} + Q^{2} + 2 P Q cos θ = P^{2}$
$\Rightarrow Q + 2 P cos θ = 0$
$\Rightarrow cos θ = - \frac{Q}{2 P}$

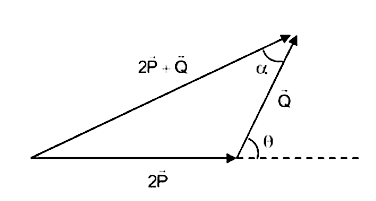
$tan α = \frac{2 P sin θ}{2 P cos θ + Q} = \infty ∴$
$[2 P cos θ + Q = 0]$
$α = 90^{\circ}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the angle between $\to P$ and the resultant of $(\to P + \to Q)$ and $(\to P - \to Q)$
AZero
B ${tan}^{- 1} (P / Q)$
C ${tan}^{- 1} (Q / P)$
D ${tan}^{- 1} (P - Q) / (P + Q)$
Question 2 - Select One
Two vectors $\to P and \to Q$ are inclined to each other at angle $θ$ . Which of the following is the unit vector perpendicular to $\to P and \to Q$ ?
A $\frac{\to P \times \to Q}{P \cdot Q}$
B $\frac{P \times ˆ Q}{sin θ}$
C $\frac{ˆ P \times ˆ Q}{P Q sin θ}$
D $\frac{ˆ P \times \to Q}{P Q sin θ}$
Question 3 - Select One
The resultant of $\to P$ and $\to Q$ is perpendicular to $\to P$ . What is the angle between $\to P$ and $\to Q$
A ${cos}^{- 1} (P / Q)$
B ${cos}^{- 1} (- P / Q)$
C ${sin}^{- 1} (P / Q)$
D ${sin}^{- 1} (- P / Q)$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 80-PHYSICS

Home
Ask Doubt
Profile