A stone of 0.5 kg mss is suspended with the help of a metre long aluminium wiere of 1 mm diameter and rotated in a horizontal plane at a rate, such that the wire make an angle of $75^{\circ}$ with the vertical. The increase in length of the wire is mm. (Take Young's modulus of aluminium
$= 7 \times 10^{10} N m^{-}, {sin 75}^{\circ} = 0.97, {cos 75}^{\circ} = 0.26$
$π = 3.14, g = 10 m / s^{2}$ )

Text Solution

Verified by Experts

The correct Answer is: $0.35$

When the stone is rotated so that it makes an angle $75^{\circ}$ with the vertical as shown in the figure below, it moves along a circle of radius $O A = r$ (say)

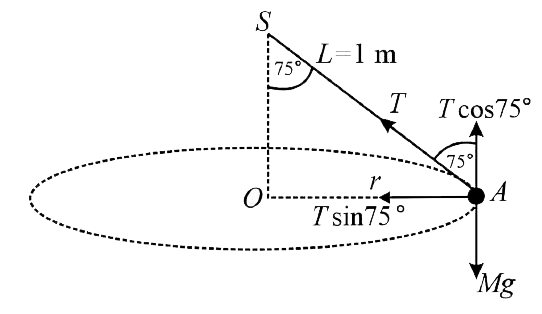
$T {cos 75}^{\circ}$ is along the vertical and balances the weight of the stone i.e.
$T {cos 75}^{\circ} = M g$
$∴ T = \frac{M g}{{cos 75}^{\circ}} = \frac{0.5 \times 10}{0.26} = 19.23 N$
Now
$Y = \frac{F / a}{l / L} = \frac{4 T L}{π D^{2} l}$
$∴ l = \frac{4 T L}{π D^{2} Y}$
$= \frac{4 \times 19.23 \times 1}{π \times {(10^{- 3})}^{2} \times 7 \times 10^{10}} = \frac{76.92}{21.98} \times 10^{- 4}$
$\approx 3.50 \times 10^{- 4} m$
..........(Rounding off to 2 decimal places)
$∴ l = 0.35 m m$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

A stone of mass $m$ tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is $Y$ , Then the increase in the length of the wire is
A $\frac{4 m g L}{π D^{2} Y}$
B $\frac{4 m g L}{π D^{2} Y sin θ}$
C $\frac{4 m g L}{π D^{2} Y cos θ}$
D $\frac{4 m g L}{π D^{2} Y tan θ}$
A stone of mass $m$ is tied to one end of a wire of length L. The diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle θ with the vertical. If Young's modulus of the wire is $Y$ , Then the increase in the length of the wire is
A $\frac{4 m g l}{π D^{2} Y}$
B $\frac{4 m g l}{π D^{2} Y sin θ}$
C $\frac{4 m g l}{π D^{2} Y cos θ}$
D $\frac{4 m g l}{π D^{2} Y tan θ}$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 112-PHYSICS

Home
Ask Doubt
Profile