An ideal gas equation can be written as P=ρRTM0 where ρ and M are resp.
mass density, mass of gas
number density, molar mass
mass density, molar mass
number density, mass of gas
The correct Answer is:C
To solve the question regarding the ideal gas equation written as P=ρRTM0, let's break it down step by step.
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = absolute temperature
Step 2: Relate Moles to Mass
The number of moles n can be expressed in terms of mass m and molar mass M0:
n=mM0
where:
- m = mass of the gas
- M0 = molar mass of the gas
Step 3: Substitute for Moles in the Ideal Gas Law
Substituting n in the ideal gas law gives:
PV=mM0RT
Step 4: Rearranging the Equation
Rearranging this equation to solve for pressure P:
P=mRTMV
Step 5: Express Mass Density
The mass density ρ is defined as:
ρ=mV
Substituting this into the pressure equation gives:
P=ρVRTM0
Step 6: Final Form of the Equation
Rearranging the equation, we arrive at:
P=ρRTM0
Conclusion
Thus, in the equation P=ρRTM0:
- ρ is the mass density of the gas,
- M0 is the molar mass of the gas,
- T is the absolute temperature,
- R is the universal gas constant.
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = absolute temperature
The number of moles n can be expressed in terms of mass m and molar mass M0:
n=mM0
where:
- m = mass of the gas
- M0 = molar mass of the gas
Substituting n in the ideal gas law gives:
PV=mM0RT
Rearranging this equation to solve for pressure P:
P=mRTMV
The mass density ρ is defined as:
ρ=mV
Substituting this into the pressure equation gives:
P=ρVRTM0
Rearranging the equation, we arrive at:
P=ρRTM0
Thus, in the equation P=ρRTM0:
- ρ is the mass density of the gas,
- M0 is the molar mass of the gas,
- T is the absolute temperature,
- R is the universal gas constant.
Similar Questions
At a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
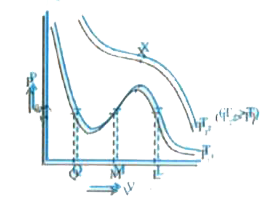
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View SolutionThe pressure of an ideal gas varies according to the law P=P0−AV2, where P0 and A are positive constants. Find the highest temperature that can be attained by the gas
View SolutionFor n moles of ideal gas, the equation of state may be written as
View SolutionAn ideal gas is found to obey the law V2T=constant. The initial pressure and temperature are P0 and T0. If gas expands such that its pressure becomes P04, then the final temperature of the gas will be
View SolutionThe van der wasl's equation of a gas is (P+aT2V)Vc=(RT+b). Where a, b, c and R are constant. If the isotherm is represented by P=AVm−BVn, where A and B depends on temperature:
View SolutionIn the given pressure - temperature (P-T) diagram, the density of an ideal gas at point A and B are ρ0 and 3ρ02respectively, then the value of X is
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe equation of state of a real gas is given by (P+aV2)(V−b)=RT
where P, V and T are pressure, volume and temperature resperature and R is the universal gas constant. The dimensions of the constant a in the above equation is
View Solution
