A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
21s
29s
31s
37 s
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the drunkard, plot the x-t graph, and determine how long it takes for him to fall into the pit located 13 meters away.
Step 1: Understand the Motion
The drunkard takes 5 steps forward and then 3 steps backward. Each step is 1 meter long and takes 1 second. Therefore, in one complete cycle (5 steps forward and 3 steps backward), he moves:
- Forward: 5 meters
- Backward: 3 meters
- Net movement in one cycle = 5 - 3 = 2 meters
The total time taken for one complete cycle is:
- Time for 5 steps forward = 5 seconds
- Time for 3 steps backward = 3 seconds
- Total time for one cycle = 5 + 3 = 8 seconds
Step 2: Calculate the Position After Each Cycle
We can calculate the position of the drunkard after each cycle:
1. After 1 cycle (8 seconds): 2 meters
2. After 2 cycles (16 seconds): 4 meters
3. After 3 cycles (24 seconds): 6 meters
4. After 4 cycles (32 seconds): 8 meters
5. After 5 cycles (40 seconds): 10 meters
6. After 6 cycles (48 seconds): 12 meters
Step 3: Determine the Next Steps
After 6 cycles, the drunkard is at 12 meters. He will take 5 steps forward (to 17 meters) and then 3 steps backward (to 14 meters). Since the pit is at 13 meters, he will fall into the pit during this phase.
Step 4: Calculate Time to Reach the Pit
- At 48 seconds, he is at 12 meters.
- At 49 seconds, he takes 1 step forward to 13 meters and falls into the pit.
Thus, the total time taken to fall into the pit is:
- 48 seconds (after 6 cycles) + 1 second = 49 seconds
Step 5: Plot the x-t Graph
1. On the x-axis, we plot the position (in meters).
2. On the y-axis, we plot the time (in seconds).
3. The graph will consist of linear segments:
- From (0, 0) to (5, 5) for the first 5 steps forward.
- From (5, 5) to (2, 8) for the 3 steps backward.
- Repeat this pattern until reaching the pit.
Final Answer
The drunkard takes 49 seconds to fall into the pit located 13 meters away from the start.
The drunkard takes 5 steps forward and then 3 steps backward. Each step is 1 meter long and takes 1 second. Therefore, in one complete cycle (5 steps forward and 3 steps backward), he moves:
- Forward: 5 meters
- Backward: 3 meters
- Net movement in one cycle = 5 - 3 = 2 meters
- Time for 5 steps forward = 5 seconds
- Time for 3 steps backward = 3 seconds
- Total time for one cycle = 5 + 3 = 8 seconds
We can calculate the position of the drunkard after each cycle:
1. After 1 cycle (8 seconds): 2 meters
2. After 2 cycles (16 seconds): 4 meters
3. After 3 cycles (24 seconds): 6 meters
4. After 4 cycles (32 seconds): 8 meters
5. After 5 cycles (40 seconds): 10 meters
6. After 6 cycles (48 seconds): 12 meters
After 6 cycles, the drunkard is at 12 meters. He will take 5 steps forward (to 17 meters) and then 3 steps backward (to 14 meters). Since the pit is at 13 meters, he will fall into the pit during this phase.
- At 48 seconds, he is at 12 meters.
- At 49 seconds, he takes 1 step forward to 13 meters and falls into the pit.
- 48 seconds (after 6 cycles) + 1 second = 49 seconds
1. On the x-axis, we plot the position (in meters).
2. On the y-axis, we plot the time (in seconds).
3. The graph will consist of linear segments:
- From (0, 0) to (5, 5) for the first 5 steps forward.
- From (5, 5) to (2, 8) for the 3 steps backward.
- Repeat this pattern until reaching the pit.
The drunkard takes 49 seconds to fall into the pit located 13 meters away from the start.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
If a cyclist takes one minute to complete half revolution on a circular path 120 m radius. What is the average velocity?
View SolutionFind the distance covered by the particles,in the following figures,(i) and (ii) while a particle travels from A to B as shown by the arrows.
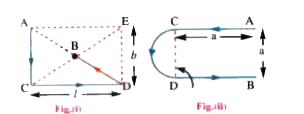
View SolutionThe ratio of the numerical values of the average velocity and average speed of a body is always
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionA proton, a deuteron and an α particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionA drunkard is walking along a stsraight road. He takes five steps forward and three steps backward and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m, away from the starting point. The drunkard will fall into the pit after.
View SolutionA drunkard waking in a barrow lane takes 5 steps forward and 3 steps backward, followed again 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s . Determine how long the drunkard takes to fall in a pit 13 m away from start.
View SolutionA drunkard waking in a borrow lane takes 6 steps forward and 4 steps backward, following againg 6 steps forward and 4 steps backward and so on Each step is 1m long and requires 1s. Determine how long the drunkard takes to fall in a pit 15m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1s. Plot the x-t graph of his motion. Determine graphically or otherwise how long the drunkard takes to fall in a pit 9 m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x−t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
View SolutionA drunkard is walking along a straight road. He takes 5 steps forward and 3 steps backward and so on. Each step is 1 m long and takes 1 s. There is a pit 11m away. The drunkard will fall into the pit after
View SolutionA drunkard is walking along a straight road. He takes five steps forward and three steps backward and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m, away from the starting point. The drunkard will fall into the pit after.
View SolutionA drunkard is walking along a stsraight road. He takes five steps forward and three steps backward and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m, away from the starting point. The drunkard will fall into the pit after.
View Solution