A helicopter is ascending vertically with a speed of 8.0ms−1. At a height of 12 m above the earth, a package is dropped from a window. How much time does it take for the package to reach the ground ?
1.23 s
3.23s
5.83s
2.53s
The correct Answer is:D
To solve the problem of how much time it takes for a package to reach the ground after being dropped from a helicopter ascending vertically, we can use the equations of motion. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
The helicopter is ascending with a speed of 8.0m/s at a height of 12m. When the package is dropped, it has the same initial velocity as the helicopter, which is 8.0m/s upwards.
Step 2: Set up the equation of motion
We will use the second equation of motion:
s=ut+12at2
Where:
- s = displacement (which will be −12m since it is falling down)
- u = initial velocity (8.0m/s upwards, but we will take it as positive)
- a = acceleration due to gravity (−10m/s2, negative because it acts downwards)
- t = time in seconds
Step 3: Substitute the values into the equation
Substituting the known values into the equation:
−12=8t−12⋅10⋅t2
This simplifies to:
−12=8t−5t2
Rearranging gives:
5t2−8t−12=0
Step 4: Solve the quadratic equation
We can solve this quadratic equation using the quadratic formula:
t=−b±√b2−4ac2a
Where a=5, b=−8, and c=−12.
Calculating the discriminant:
b2−4ac=(−8)2−4⋅5⋅(−12)=64+240=304
Now substituting back into the quadratic formula:
t=−(−8)±√3042⋅5=8±√30410
Step 5: Calculate the value of t
Calculating √304:
√304≈17.43
Thus:
t=8±17.4310
Calculating the two possible values of t:
1. t=8+17.4310=25.4310≈2.543s
2. t=8−17.4310=−9.4310≈−0.943s (not physically meaningful)
Final Answer
The time it takes for the package to reach the ground is approximately 2.54s.
---
The helicopter is ascending with a speed of 8.0m/s at a height of 12m. When the package is dropped, it has the same initial velocity as the helicopter, which is 8.0m/s upwards.
We will use the second equation of motion:
s=ut+12at2
Where:
- s = displacement (which will be −12m since it is falling down)
- u = initial velocity (8.0m/s upwards, but we will take it as positive)
- a = acceleration due to gravity (−10m/s2, negative because it acts downwards)
- t = time in seconds
Substituting the known values into the equation:
−12=8t−12⋅10⋅t2
This simplifies to:
−12=8t−5t2
Rearranging gives:
5t2−8t−12=0
We can solve this quadratic equation using the quadratic formula:
t=−b±√b2−4ac2a
Where a=5, b=−8, and c=−12.
b2−4ac=(−8)2−4⋅5⋅(−12)=64+240=304
t=−(−8)±√3042⋅5=8±√30410
Calculating √304:
√304≈17.43
Thus:
t=8±17.4310
1. t=8+17.4310=25.4310≈2.543s
2. t=8−17.4310=−9.4310≈−0.943s (not physically meaningful)
The time it takes for the package to reach the ground is approximately 2.54s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A rock is dropped from an 80- meter cliff. How long does it take to reach the ground ?
View SolutionA balloon is ascending at the constant rate of 9.8m/sec at a height of 98m above the ground a packet is dropped from it. If time taken by the packet to reach the ground is (1+√3λ)sec. Find λ.
(Use g=9.8m/s2)
View Solution
Knowledge Check
Body 1 of mass M is dropped from a height of 1 m and body 2 of mass 3 M is dropped from a height of 9 m. Ratio of time taken by bodies 1 and 2 to reach the ground is
A1:1B1:3C3:1D9:1
A helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
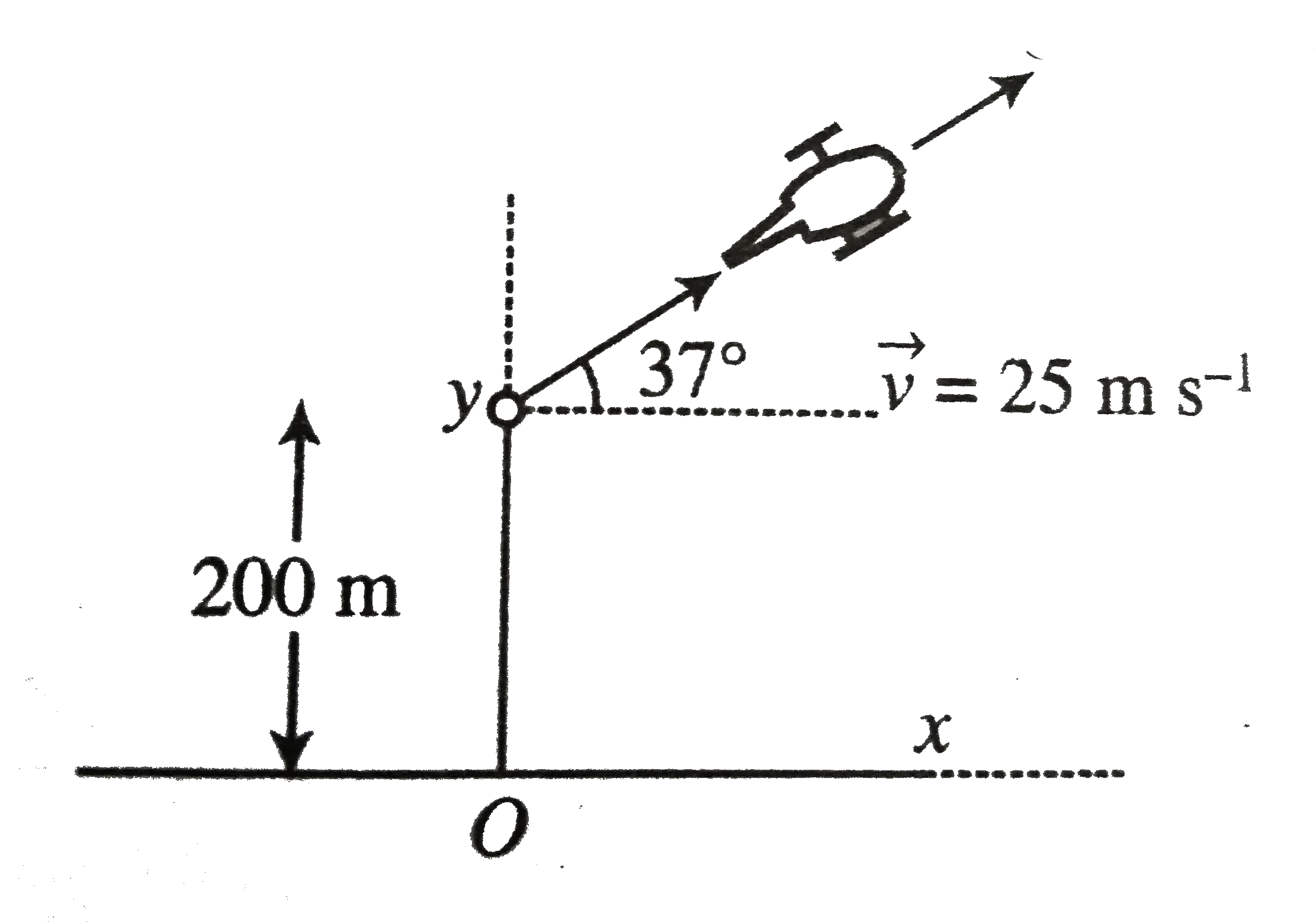
The distance of the point O where the package lands is
View SolutionA helicopter rises from rest on the ground vertically upwards with a constant acceleration g. A food packet is dropped from the helicopter when is at a height h. The time taken by the packet to reach the ground is close to [ g is the acceeration due to gravity] :
View SolutionA balloon rises with uniform velocity of 10ms−1. When the balloon is at a height of 75 m if a stone is dropped from it the time taken by it to reach the ground is
View SolutionA helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
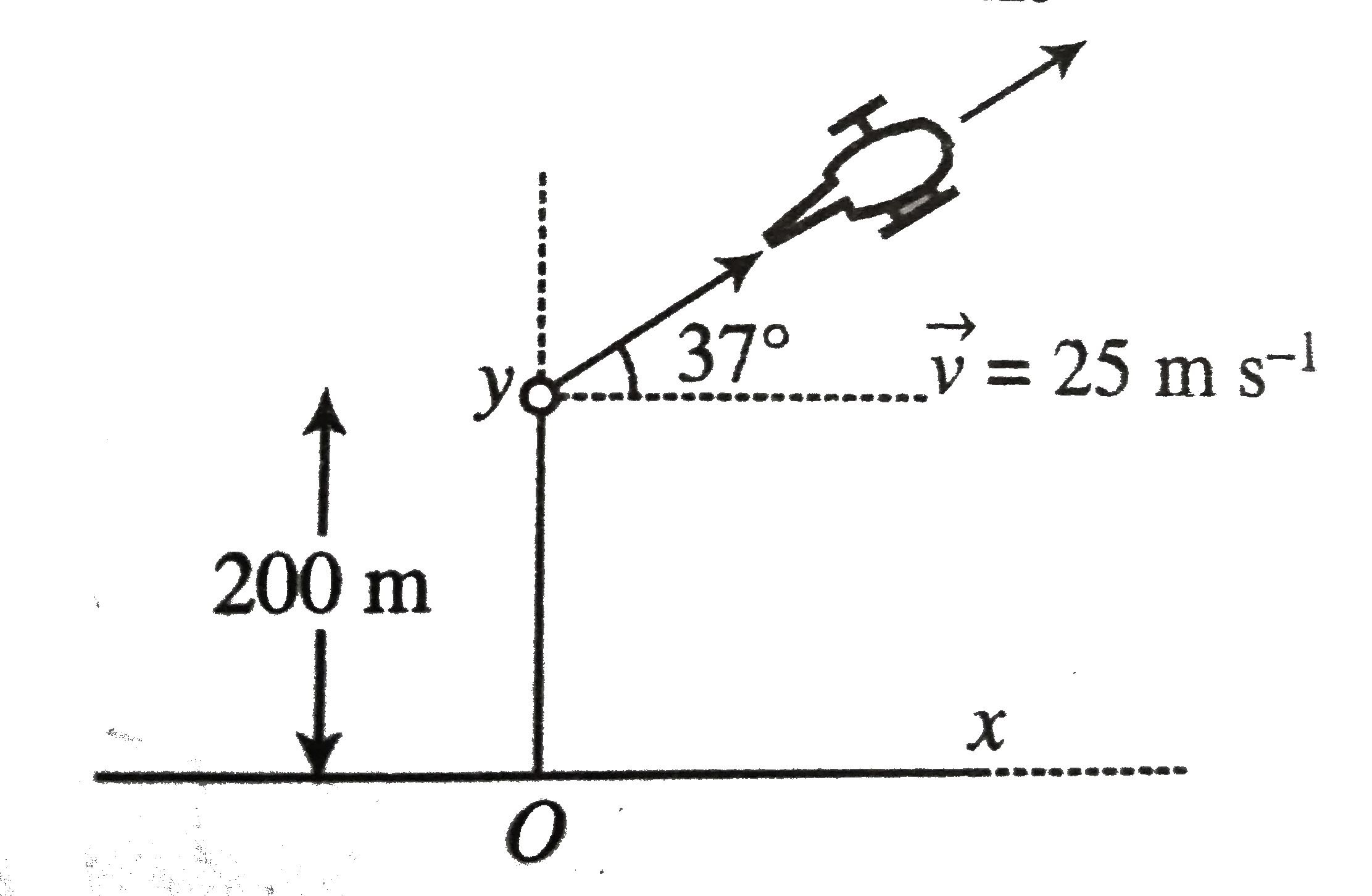
If the helicopter flies at constant velocity, find the x and y coordinates of the location of the helicopter when the package lands.
View SolutionA helicopter is flying horizontally at an altitude of 2km with a speed of 100ms−1 . A packet is dropped from it. The horizontal distance between the point where the packet is dropped and the point where it hits the ground is (g=10ms−2)
View Solution(A):A balloon ascends from the surface of earth with constant speed.When it was at a height 50m above the ground,a packet is dropped from it .To an abserver on the balloon,the displacement of the packet,from the moment it is dropped to the moment it reaches the surface of earth is 50m.
(R ):Displacement vector does not depend upon the reference frame used to measure it.
View SolutionHow long does it take a brick to reach the ground if dropped from a height of 65 m? What will be its velocity just before it reaches the ground ?
View Solution
