Question

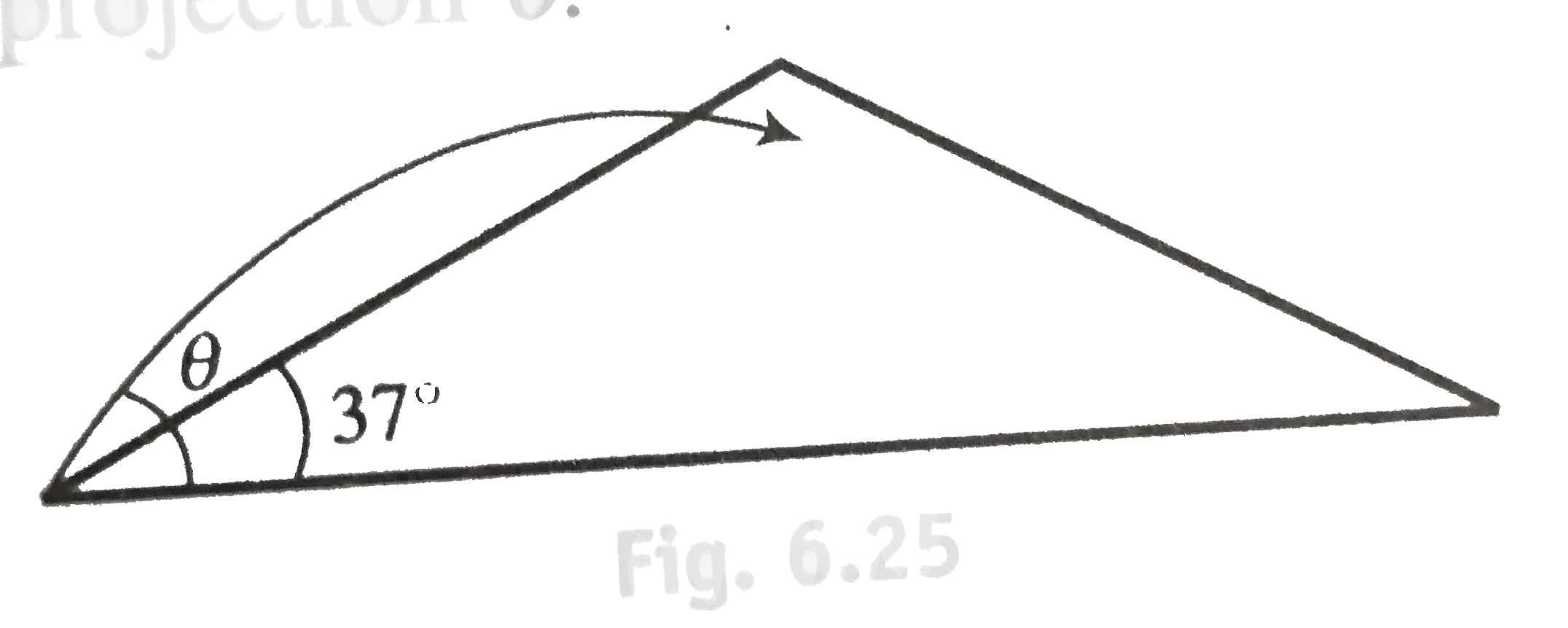
A gun is mounted on a gun carriage movable on a smooth plane the gun is elevated at an angle $\alpha$ to the horizontal . A shot, fired leaves the gun in a direction inclined at an angle $\theta$ to the horizontal . If the mass of the gum and its carriage be n times that of short , find $\tan \theta :\tan \alpha$ .

Explanation

To solve the problem, we need to analyze the motion of the gun and the projectile fired from it. We will use the principles of momentum conservation and the relationships between the angles and velocities involved.

1. Identify the Masses:
- Let the mass of the shot be \( m \).
- The mass of the gun and its carriage is \( n \times m \).

2. Define the Angles:
- The gun is elevated at an angle \( \alpha \) to the horizontal.
- The shot leaves the gun at an angle \( \theta \) to the horizontal.

3. Components of Velocity:
- When the shot is fired, it has a velocity \( v \) which can be resolved into two components:
- Horizontal component: \( v \cos \alpha \)
- Vertical component: \( v \sin \alpha \)

4. Velocity of the Gun:
- Since the gun is mounted on a carriage that can move, when the shot is fired, the gun will also have a horizontal velocity \( v_0 \) due to the recoil.
- The horizontal motion of the gun and the shot must satisfy the conservation of momentum.

5. Conservation of Momentum:
- Before firing, the total momentum is zero (the system is at rest).
- After firing, the momentum of the shot plus the momentum of the gun must still equal zero:
\( m(v \cos \theta) - n m v_0 = 0 \)
- Rearranging gives:
\( v \cos \theta = n v_0 \)

6. Relate \( v_0 \) to \( v \):
- The horizontal velocity of the gun after firing can be expressed as:
\( v_0 = \frac{v \cos \alpha}{n + 1} \)
- Substitute this into the momentum equation:
\( v \cos \theta = n \left(\frac{v \cos \alpha}{n + 1}\right) \)

7. Simplifying the Equation:
- Cancel \( v \) (assuming \( v \neq 0 \)):
\( \cos \theta = \frac{n \cos \alpha}{n + 1} \)

8. Finding \( \tan \theta \) and \( \tan \alpha \):
- From the definition of tangent, we have:
\( \tan \theta = \frac{\sin \theta}{\cos \theta} \quad \text{and} \quad \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \)
- Using the relationship we derived, we can express \( \tan \theta \):
\( \tan \theta = \frac{\sin \theta}{\frac{n \cos \alpha}{n + 1}} = \frac{(n + 1) \sin \theta}{n \cos \alpha} \)

9. Final Ratio:
- The ratio \( \frac{\tan \theta}{\tan \alpha} \) can now be expressed as:
\( \frac{\tan \theta}{\tan \alpha} = \frac{(n + 1) \sin \theta \cos \alpha}{n \sin \alpha \cos \theta} \)
- Since we know \( \sin \theta \) and \( \cos \theta \) can be related through the angles, we can derive the final relation.

10. Conclusion:
- After simplification, we find:
\( \frac{\tan \theta}{\tan \alpha} = 1 \)
- Thus, \( \tan \theta : \tan \alpha = 1 : 1 \).