Dielectric constant has the same dimensions as
Stress
Strain
Electric capacity
Electric permittivity
The correct Answer is:B
To solve the question regarding the dielectric constant and its dimensions, we can follow these steps:
1. Understanding Dielectric Constant: The dielectric constant (k) of a material is defined as the ratio of the capacitance of a capacitor filled with the dielectric material to the capacitance of the same capacitor when it is filled with air (or vacuum). Mathematically, it can be expressed as:
k=CdielectricCair
2. Nature of Dielectric Constant: Since the dielectric constant is a ratio of two capacitances, it is a dimensionless quantity. Capacitance itself has units (Farads), but when you take a ratio of two capacitances, the units cancel out, leaving a pure number without any dimensions.
3. Identifying Dimensionless Quantities: To find a quantity that has the same dimensions as the dielectric constant, we need to look for other dimensionless quantities.
4. Example of Dimensionless Quantities: One common example of a dimensionless quantity is strain. Strain is defined as the change in length divided by the original length:
Strain=ΔLL
Here, both ΔL (change in length) and L (original length) have the same dimensions (length), so when you take their ratio, the dimensions cancel out, making strain a dimensionless quantity.
5. Conclusion: Since the dielectric constant is dimensionless and strain is also dimensionless, we conclude that the dielectric constant has the same dimensions as strain.
Final Answer:
The dielectric constant has the same dimensions as strain, which is a dimensionless quantity.
---
k=CdielectricCair
Strain=ΔLL
Here, both ΔL (change in length) and L (original length) have the same dimensions (length), so when you take their ratio, the dimensions cancel out, making strain a dimensionless quantity.
The dielectric constant has the same dimensions as strain, which is a dimensionless quantity.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE - II
61 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
Similar Questions
Planck constant has the same dimensions as
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates
View Solution
Knowledge Check
A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the platesAC=ε0Ad(K+34K)BC=ε0Ad(2KK+3)CC=ε0Ad(KK+3)DC=ε0Ad(4KK+3)
Assertion : The dimensional formula for product of resistance and conductance is same as for dielectric constant.
Reason : both have dimensions of time constant.
View SolutionWhich pair has the same dimensions?
View SolutionIntensity of Magnetization has the same dimensions as
View SolutionIn the figure shown capacitors A and B of capacitance C are in steady state. A dielectric slab of dielectric constant K=2 and dimensions equal to the inner dimensions of the capcitors is inserted in the space between the plate of the capacitor B. In steady state choose the correct options.
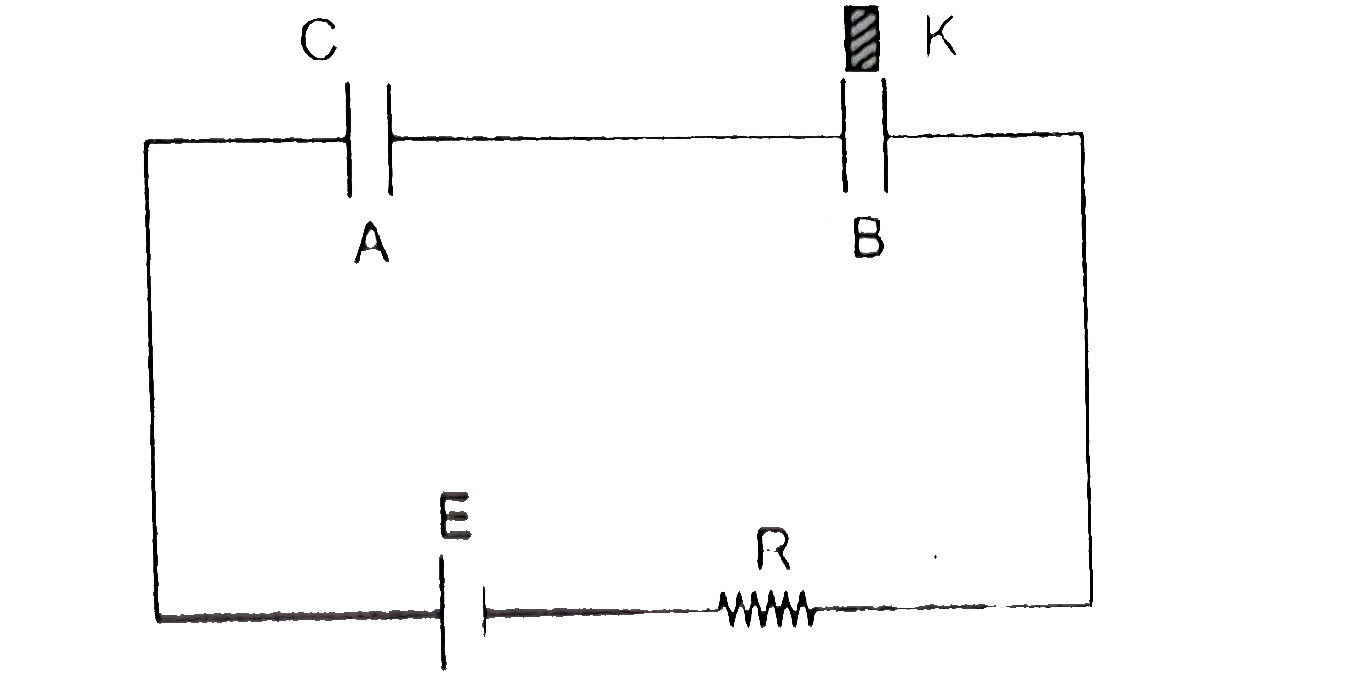
View SolutionGas constant 'R' has dimensions :
View SolutionThe rate constant of a reaction has same dimensions as rate of reaction The reaction is of
View SolutionSurface tension has the same dimensions as that of
View Solution
