A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates
To solve the problem of how the capacitance changes when a dielectric slab is inserted between the plates of a parallel plate capacitor, we will follow these steps:
1. Identify the Initial Capacitance:
The initial capacitance C1 of a parallel plate capacitor without any dielectric is given by the formula:
C1=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
2. Determine the Configuration with the Dielectric:
When a dielectric slab of thickness 34d and dielectric constant K is inserted, we can treat the capacitor as two capacitors in series:
- Capacitor A (with air): thickness d−34d=14d
- Capacitor B (with dielectric): thickness 34d
3. Calculate the Capacitance of Each Section:
- For Capacitor A (air):
CA=ε0A14d=4ε0Ad=4C1
- For Capacitor B (dielectric):
CB=Kε0A34d=4Kε0A3d
4. Combine the Two Capacitors in Series:
The total capacitance C2 of two capacitors in series is given by:
1C2=1CA+1CB
Substituting the values:
1C2=14C1+34KC1
5. Simplify the Expression:
To combine the fractions:
1C2=K+34KC1
Therefore,
C2=4KC1K+3
6. Final Result:
The final capacitance when the dielectric slab is inserted is:
C2=4KK+3C1
The initial capacitance C1 of a parallel plate capacitor without any dielectric is given by the formula:
C1=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
When a dielectric slab of thickness 34d and dielectric constant K is inserted, we can treat the capacitor as two capacitors in series:
- Capacitor A (with air): thickness d−34d=14d
- Capacitor B (with dielectric): thickness 34d
- For Capacitor A (air):
CA=ε0A14d=4ε0Ad=4C1
- For Capacitor B (dielectric):
CB=Kε0A34d=4Kε0A3d
The total capacitance C2 of two capacitors in series is given by:
1C2=1CA+1CB
Substituting the values:
1C2=14C1+34KC1
To combine the fractions:
1C2=K+34KC1
Therefore,
C2=4KC1K+3
The final capacitance when the dielectric slab is inserted is:
C2=4KK+3C1
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
- MAGNETISM AND MATTERBOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise
25 Videos
Similar Questions
A slab of materail of dielectric constant K has the same area as the plates of a parallel plate capacitor but has thickness d/2, where d is the separation between the plates. Find the expression for the capacitance when the slab is inserted between the plates.
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionA parallel plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and electric constant K is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates. Find the capacitance of the system.
IF K=2, for what value of t/d will the capacitance of the system be 3/2 times that of the air capacitor? Calculate the energy in the two cases and account for the energy change.
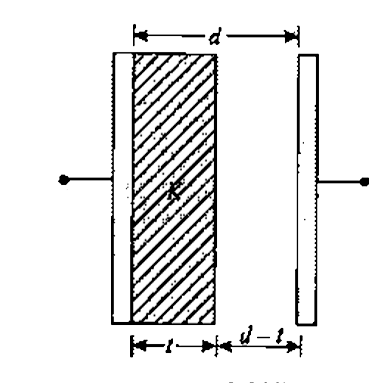
View SolutionA slab of copper of thickness y is inserted between the plates of parallel plate capacitor as shown in figure. The separation between the plates is d. If y=d4, then the ratio of capacitance of the capacitor after nd before inserting the slab is

View SolutionA slab of copper of thickness b is inserted in between the plates of parallel plate capacitor as shown in figure. The separation of the plate is d. If b=d/2, then the ratio of capacities of the capacitor after and before inserting that slab will be

View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View SolutionA dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
A. become zero
B. remains the same
C. decrease
D. increase
View Solution
